
【題目】如圖,在△ABC中,以AB為直徑的⊙O交BC于點D,交AC于點E,連結DE,且BD=DE,過點B作BP∥DE,交⊙O于點P,連結OP.
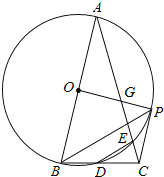
(1)求證:AB=AC;
(2)若∠A=30°,求∠BOP的度數.
【答案】(1)見解析;(2)∠BOP=90°
【解析】
(1)連結AD,根據直徑所對的圓周角為直角得到∠ADB=90°,求出∠BAD=∠CAD,△ADB≌△ADC即可;
(2)根據等腰三角形的性質和三角形內角和定理可計算出∠ABC=75°,再根據圓內接四邊形的性質得到∠EDC=∠BAC=30°,然后利用平行線的性質得到∠PBC=∠EDC=30°,所以∠OBP=∠ABC-∠PBC=45°,于是可判斷△OBP為等腰直角三角形,則∠BOP=90°.
(1)證明:連接AD,
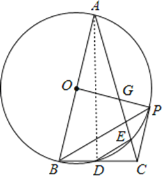
∵BD=DE,
∴![]()
∴∠BAD=∠CAD,
∵AB為⊙O的直徑,
∴∠ADB=90°=∠CDA,
在△ADB和△ADC中
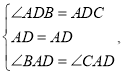
∴△ADB≌△ADC(ASA),
∵AB=AC;
(2)解:∵∠BAC=30°,AB=AC,
∴∠ABC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵四邊形ABDE為圓O的內接四邊形,
∴∠EDC=∠BAC=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠OBP=∠ABC﹣∠PBC=45°,
∵OB=OP,
∴△OBP為等腰直角三角形,
∴∠BOP=90°.


科目:初中數學 來源: 題型:
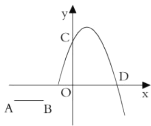
【題目】如圖,已知![]() ,線段
,線段![]() 與
與![]() 軸平行,且
軸平行,且![]() ,拋物線
,拋物線![]() 經過點
經過點![]() 和
和![]() ,若線段
,若線段![]() 以每秒2個單位長度的速度向下平移,設平移的時間為
以每秒2個單位長度的速度向下平移,設平移的時間為![]() (秒).若拋物線與線段
(秒).若拋物線與線段![]() 有公共點,則
有公共點,則![]() 的取值范圍是( )
的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程:2(x﹣k)=x﹣4①和關于x的一元二次方程:(k﹣1)x2+2mx+(3﹣k)+n=0②(k、m、n均為實數),方程①的解為非正數.
(1)求k的取值范圍;
(2)如果方程②的解為負整數,k﹣m=2,2k﹣n=6且k為整數,求整數m的值;
(3)當方程②有兩個實數根x1、x2,滿足(x1+x2)(x1﹣x2)+2m(x1﹣x2+m)=n+5,且k為正整數,試判斷|m|≤2是否成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《中國漢字聽寫大會》 喚醒了很多人對文字基本功的重視和對漢字文化的學習,某校組織了一次全校2000名學生參加的“漢字聽寫大會”海選比賽,賽后發現所有參賽學生的成績均不低于50分,為了更好地了解本次海選比賽的成績分布情況,隨機抽取了其中200名學生的海選比賽成績(成績![]() 取整數,總分100分)作為樣本進行整理,得到下列統計圖表:
取整數,總分100分)作為樣本進行整理,得到下列統計圖表:
抽取的200名學生海選成績分組表
組別 | 海選成績 |
A組 |
|
B組 |
|
C組 |
|
D組 |
|
E組 |
|

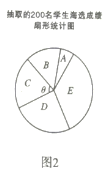
請根據所給信息,解答下列問題
(1)請把圖1中的條形統計圖補充完整;
(2)在圖2的扇形統計圖中,表示![]() 組扇形的圓心角
組扇形的圓心角![]() 的度數為_______度;
的度數為_______度;
(3)規定海選成績在90分以上(包括90分)記為“優等”,請估計該校參加這次海選比賽的2000名學生中成績“優等”的有多少人;
(4)經過統計發現,在![]() 組中,有2位男生和2位女生獲得了滿分,如果從這4人中挑選2人代表學校參加比賽,請用樹狀圖或列表法求出所選兩人正好是一男一女的概率是多少?
組中,有2位男生和2位女生獲得了滿分,如果從這4人中挑選2人代表學校參加比賽,請用樹狀圖或列表法求出所選兩人正好是一男一女的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+3與x軸交于A(﹣3,0),B(l,0)兩點,與y軸交于點C.
(1)求拋物線的解析式;
(2)點P是拋物線上的動點,且滿足S△PAO=2S△PCO,求出P點的坐標;
(3)連接BC,點E是x軸一動點,點F是拋物線上一動點,若以B、C、E、F為頂點的四邊形是平行四邊形時,請直接寫出點F的坐標.
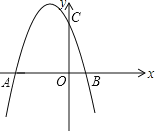
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學共有3個一樣規模的大餐廳和2個一樣規模的小餐廳,經過測試同時開放2個大餐廳和1個小餐廳,可供3000名學生就餐;同時開放1個大餐廳,1個小餐廳,可供1700名學生就餐.
(1)請問1個大餐廳、1個小餐廳分別可供多少名學生就餐.
(2)如果3個大餐廳和2個小餐廳全部開放,那么能否供全校4500名學生就餐?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某快遞公司每天上午9:00-10:00為集中攬件和派件時段,甲倉庫用來攬收快件,乙倉庫用來派發快件,該時段內甲、乙兩倉庫的快件數量y(件)與時間x(分)之間的函數圖象如圖所示,那么當兩倉庫快遞件數相同時,此刻的時間為__________;
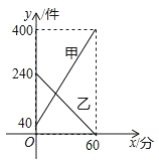
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】撫順市某校想知道學生對“遙遠的赫圖阿拉”,“旗袍故里”等家鄉旅游品牌的了解程度,隨機抽取了部分學生進行問卷調查,問卷有四個選項(每位被調查的學生必選且只選一項)A.十分了解,B.了解較多,C.了解較少,D.不知道.將調查的結果繪制成如下兩幅不完整的統計圖,請根據兩幅統計圖中的信息回答下列問題:
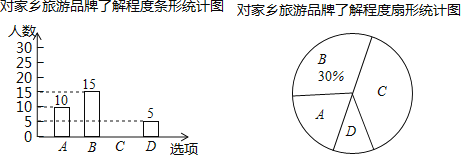
(1)本次調查了多少名學生?
(2)補全條形統計圖;
(3)該校共有500名學生,請你估計“十分了解”的學生有多少名?
(4)在被調查“十分了解”的學生中有四名學生會干部,他們中有3名男生和1名女生,學校想從這4人中任選兩人做家鄉旅游品牌宣傳員,請用列表或畫樹狀圖法求出被選中的兩人恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種型號的電熱水器工作過程如下:在接通電源以后,從初始溫度20![]() 下加熱水箱中的水,當水溫達到設定溫度60
下加熱水箱中的水,當水溫達到設定溫度60![]() 時,加熱停止;此后水箱中的水溫開始逐漸下降,當下降到保溫溫度30
時,加熱停止;此后水箱中的水溫開始逐漸下降,當下降到保溫溫度30![]() 時,再次自動加熱水箱中的水至60
時,再次自動加熱水箱中的水至60![]() ,加熱停止;當水箱中的水溫下降到30
,加熱停止;當水箱中的水溫下降到30![]() 時,再次自動加熱,……,按照以上方式不斷循環.小宇根據學習函數的經驗,對該型號電熱水器水箱中的水溫隨時間變化的規律進行了探究,發現水溫
時,再次自動加熱,……,按照以上方式不斷循環.小宇根據學習函數的經驗,對該型號電熱水器水箱中的水溫隨時間變化的規律進行了探究,發現水溫![]() 是時間
是時間![]() 的函數,其中
的函數,其中![]() (單位:
(單位:![]() )表示水箱中水的溫度,
)表示水箱中水的溫度,![]() (單位:
(單位:![]() )表示接通電源后的時間.下面是小宇的探究過程,請補充完整:
)表示接通電源后的時間.下面是小宇的探究過程,請補充完整:
(1)小宇記錄了從初始溫度20![]() 第一次加熱至設定溫度60
第一次加熱至設定溫度60![]() ,之后水溫冷卻至保溫溫度30
,之后水溫冷卻至保溫溫度30![]() 的過程中,
的過程中,![]() 隨
隨![]() 的變化情況,如下表所示:
的變化情況,如下表所示:
接通電源后的時間 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | … |
水箱中水的溫度 | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
①請寫出一個符合加熱階段![]() 與
與![]() 關系的函數解析式______________;
關系的函數解析式______________;
②根據該電熱水器的工作特點,當第二次加熱至設定溫度60![]() 時,距離接通電源的時間
時,距離接通電源的時間![]() 為________
為________![]() .
.
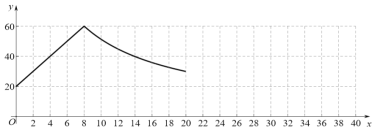
(2)根據上述的表格,小宇畫出了當![]() 時的函數圖象,請根據該電熱水器的工作特點,幫他畫出當
時的函數圖象,請根據該電熱水器的工作特點,幫他畫出當![]() 時的函數圖象.
時的函數圖象.
(3)已知適宜人體沐浴的水溫約為![]() ,小宇在上午8點整接通電源,水箱中水溫為20
,小宇在上午8點整接通電源,水箱中水溫為20![]() ,熱水器開始按上述模式工作,若不考慮其他因素的影響,請問在上午9點30分時,熱水器的水溫______(填“是”或“否”)適合他沐浴,理由是_________________.
,熱水器開始按上述模式工作,若不考慮其他因素的影響,請問在上午9點30分時,熱水器的水溫______(填“是”或“否”)適合他沐浴,理由是_________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com