Question

【題目】如圖1，在正方形ABCD中，E，F，G，H分別為邊AB，BC，CD，DA上的點，HA=EB=FC=GD，連接EG，FH，交點為O．
（1）如圖2，連接EF，FG，GH，HE，試判斷四邊形EFGH的形狀，并證明你的結論；
（2）將正方形ABCD沿線段EG，HF剪開，再把得到的四個四邊形按圖3的方式拼接成一個四邊形．若正方形ABCD的邊長為3cm，HA=EB=FC=GD=1cm，則圖3中陰影部分的面積為多少？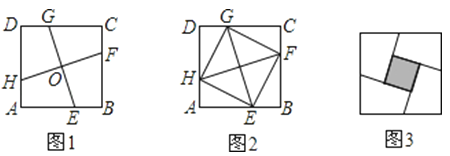

Answer 1

【答案】解：（1）四邊形EFGH是正方形．
證明：∵四邊形ABCD是正方形，
∴∠A=∠B=∠C=∠D=90°，AB=BC=CD=DA，
∵HA=EB=FC=GD，
∴AE=BF=CG=DH，
∴△AEH≌△BFE≌△CGF≌△DHG，
∴EF=FG=GH=HE，
∴四邊形EFGH是菱形，
∵△DHG≌△AEH，
∴∠DHG=∠AEH，
∵∠AEH+∠AHE=90°，
∴∠DHG+∠AHE=90°，
∴∠GHE=90°，
∴四邊形EFGH是正方形．
（2）

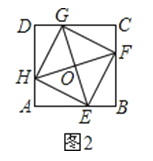
∵HA=EB=FC=GD=1，AB=BC=CD=AD=3，
∴GF=EF=EH=GH= =，
∵由（1）知，四邊形EFGH是正方形，
∴GO=OF，∠GOF=90°，
由勾股定理得：GO=OF=，
∵S四邊形FCGO=×1×2+××=，
∴S陰影= (+)2﹣S四邊形FCGO×4=10﹣9=1．
【解析】（1）先證明△AEH≌△BFE≌△CGF≌△DHG，可得出四邊形GHEF是菱形，再根據全等三角形角之間的關系，又可得出菱形的一個角是直角，那么就可得出四邊形GHEF是正方形．
（2）根據已知條件，可以知道重新拼成的四邊形是正方形（因為正方形GHEF的對角線翻到了外邊，做了新拼成的正方形的邊長），利用勾股定理求出GF和GO、FO的長，所的面積是10減去4個四邊形GOFC的面積就是陰影部分的面積．