
【題目】已知如圖,矩形OABC的長OA=![]() , 寬OC=1,將△AOC沿AC翻折得△APC.
, 寬OC=1,將△AOC沿AC翻折得△APC.
(1)求∠PCB的度數(shù);
(2)若P,A兩點(diǎn)在拋物線y=![]() x2+bx+c上,求b,c的值,并說明點(diǎn)C在此拋物線上;
x2+bx+c上,求b,c的值,并說明點(diǎn)C在此拋物線上;
(3)題(2)中的拋物線與矩形OABC邊CB相交于點(diǎn)D,與x軸相交于另外一點(diǎn)E,若點(diǎn)M是x軸上的點(diǎn),N是y軸上的點(diǎn),以點(diǎn)E、M、D、N為頂點(diǎn)的四邊形是平行四邊形,試求點(diǎn)M、N的坐標(biāo).



【答案】(1)30°; (2)當(dāng)x=0時(shí),y=1,故C(0,1)在拋物線的圖象上;(3)見解析
【解析】(1)根據(jù)OC、OA的長,可求得∠OCA=∠ACP=60°(折疊的性質(zhì)),∠BCA=∠OAC=30°,由此可判斷出∠PCB的度數(shù).
(2)過P作PQ⊥OA于Q,在Rt△PAQ中,易知PA=OA=3,而∠PAO=2∠PAC=60°,即可求出AQ、PQ的長,進(jìn)而可得到點(diǎn)P的坐標(biāo),將P、A坐標(biāo)代入拋物線的解析式中,即可得到b、c的值,從而確定拋物線的解析式,然后將C點(diǎn)坐標(biāo)代入拋物線的解析式中進(jìn)行驗(yàn)證即可.
(3)根據(jù)拋物線的解析式易求得C、D、E點(diǎn)的坐標(biāo),然后分兩種情況考慮:
①DE是平行四邊形的對角線,由于CD∥x軸,且C在y軸上,若過D作直線CE的平行線,那么此直線與x軸的交點(diǎn)即為M點(diǎn),而N點(diǎn)即為C點(diǎn),D、E的坐標(biāo)已經(jīng)求得,結(jié)合平行四邊形的性質(zhì)即可得到點(diǎn)M的坐標(biāo),而C點(diǎn)坐標(biāo)已知,即可得到N點(diǎn)的坐標(biāo);
②DE是平行四邊形的邊,由于A在x軸上,過A作DE的平行線,與y軸的交點(diǎn)即為N點(diǎn),而M點(diǎn)即為A點(diǎn);易求得∠DEA的度數(shù),即可得到∠NAO的度數(shù),已知OA的長,通過解直角三角形可求得ON的值,從而確定N點(diǎn)的坐標(biāo),而M點(diǎn)與A點(diǎn)重合,其坐標(biāo)已知;
同理,由于C在y軸上,且CD∥x軸,過C作DE的平行線,也可找到符合條件的M、N點(diǎn),解法同上.
解:(1)在Rt△OAC中,OA=![]() ,OC=1,則∠OAC=30°,∠OCA=60°;
,OC=1,則∠OAC=30°,∠OCA=60°;
根據(jù)折疊的性質(zhì)知:OA=AP=![]() ,∠ACO=∠ACP=60°;
,∠ACO=∠ACP=60°;
∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°.
(2)過P作PQ⊥OA于Q;

Rt△PAQ中,∠PAQ=60°,AP=![]() ;
;
∴OQ=AQ=![]() ,PQ=
,PQ=![]() ,
,
所以P(![]() ,
, ![]() );
);
將P、A代入拋物線的表達(dá)式中,得: 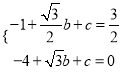 ,
,
解得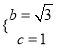 ;
;
即y=![]() x2+
x2+![]() x+1;
x+1;
當(dāng)x=0時(shí),y=1,故C(0,1)在拋物線的圖象上.
(3)①若DE是平行四邊形的對角線,點(diǎn)C在y軸上,CD平行x軸,
∴過點(diǎn)D作DM∥CE交x軸于M,則四邊形EMDC為平行四邊形,
把y=1代入拋物線解析式得點(diǎn)D的坐標(biāo)為(![]() ,1)
,1)
把y=0代入拋物線解析式得點(diǎn)E的坐標(biāo)為(![]() ,0)
,0)
∴M(![]() ,0);N點(diǎn)即為C點(diǎn),坐標(biāo)是N(0,1);
,0);N點(diǎn)即為C點(diǎn),坐標(biāo)是N(0,1);
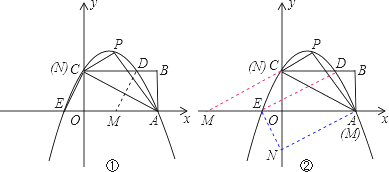
②若DE是平行四邊形的邊,
過點(diǎn)A作AN∥DE交y軸于N,四邊形DANE是平行四邊形,
∴DE=AN=![]() =
=![]() =2,
=2,
∴∠EAN=30°,∠DEA=30°,
∴M(![]() ,0),N(0,-1)
,0),N(0,-1)
同理過點(diǎn)C作CM∥DE交y軸于N,四邊形CMDE是平行四邊形,
∴M(-![]() ,0),N(0,1).
,0),N(0,1).
“點(diǎn)睛”此題考查了矩形的性質(zhì)、圖形的翻折變換、二次函數(shù)解析式的確定、平行四邊形的判定和性質(zhì)等知識,同時(shí)考查了分類討論的數(shù)學(xué)思想,難度較大.


 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖,直徑是50cm圓柱形油槽裝入油后,油深CD為15cm,求油面寬度AB的長.

(2)如圖,在△ABC中,D、E分別是AB、AC的中點(diǎn),BE=2DE,過點(diǎn)C作CF∥BE交DE的延長線于F,連接CD.
①求證:四邊形BCFE是菱形;
②在不添加任何輔助線和字母的情況下,請直接寫出圖中與△BEC面積相等的所有三角形(不包括△BEC).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一組數(shù):8,9,7,10,6,9,9,6,則這組數(shù)的中位數(shù)與眾數(shù)的和是( )
A.16.5
B.17
C.17.5
D.18
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】設(shè)x是有理數(shù),那么下列各式中一定表示正數(shù)的是( )
A.2018xB.x+2018C.|2018x|D.|x|+2018
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系內(nèi),二次函數(shù)圖象的頂點(diǎn)為A(1,﹣4),且過點(diǎn)B(3,0).
(1)求該二次函數(shù)的解析式;
(2)將該二次函數(shù)圖象向右平移幾個(gè)單位,可使平移后所得圖象經(jīng)過坐標(biāo)原點(diǎn)?并直接寫出平移后所得圖象與x軸的另一個(gè)交點(diǎn)的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:在△ABC中,AC=BC,∠ACB=90°,點(diǎn)D是AB的中點(diǎn),點(diǎn)E是AB邊上一點(diǎn).
(1)如圖1,BF垂直CE于點(diǎn)F,交CD于點(diǎn)G,證明:AE=CG;
(2)如圖2,作AH垂直于CE的延長線,垂足為H,交CD的延長線于點(diǎn)M,則圖中與BE相等的線段是 ,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】直線l外有一定點(diǎn)A,點(diǎn)A到直線l的距離是7cm,B是直線l上的任意一點(diǎn),則線段AB的長度可能是________cm.(寫出一個(gè)滿足條件的值即可)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,二次函數(shù)
中,二次函數(shù)![]() 的圖象經(jīng)過點(diǎn)
的圖象經(jīng)過點(diǎn)![]() ,且當(dāng)
,且當(dāng)![]() 和
和![]() 時(shí)所對應(yīng)的函數(shù)值相等.一次函數(shù)
時(shí)所對應(yīng)的函數(shù)值相等.一次函數(shù)![]() 與二次函數(shù)
與二次函數(shù)![]() 的圖象分別交于
的圖象分別交于![]() ,
, ![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 在第一象限.
在第一象限.

(![]() )求二次函數(shù)
)求二次函數(shù)![]() 的表達(dá)式.
的表達(dá)式.
(![]() )連接
)連接![]() ,求
,求![]() 的長.
的長.
(![]() )連接
)連接![]() ,
, ![]() 是線段
是線段![]() 得中點(diǎn),將點(diǎn)
得中點(diǎn),將點(diǎn)![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn)
旋轉(zhuǎn)![]() 得到點(diǎn)
得到點(diǎn)![]() ,連接
,連接![]() ,
, ![]() ,判斷四邊形
,判斷四邊形![]() 的性狀,并證明你的結(jié)論.
的性狀,并證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com