
【題目】【提出問題】
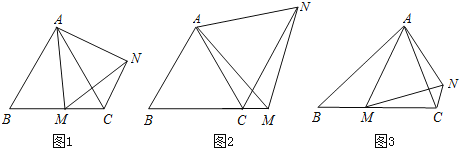
(1)如圖1,在等邊△ABC中,點M是BC上的任意一點(不含端點B、C),連結AM,以AM為邊作等邊△AMN,連結CN.求證:∠ABC=∠ACN.
【類比探究】
(2)如圖2,在等邊△ABC中,點M是BC延長線上的任意一點(不含端點C),其它條件不變,(1)中結論∠ABC=∠ACN還成立嗎?請說明理由.
【拓展延伸】
(3)如圖3,在等腰△ABC中,BA=BC,點M是BC上的任意一點(不含端點B、C),連結AM,以AM為邊作等腰△AMN,使頂角∠AMN=∠ABC.連結CN.試探究∠ABC與∠ACN的數量關系,并說明理由.
【答案】(1)見解析;(2)結論∠ABC=∠ACN仍成立;理由見解析;(3)∠ABC=∠ACN.
【解析】
試題分析:(1)利用SAS可證明△BAM≌△CAN,繼而得出結論;
(2)也可以通過證明△BAM≌△CAN,得出結論,和(1)的思路完全一樣.
(3)首先得出∠BAC=∠MAN,從而判定△ABC∽△AMN,得到![]() =
=![]() ,根據∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,從而判定△BAM∽△CAN,得出結論.
,根據∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,從而判定△BAM∽△CAN,得出結論.
(1)證明:∵△ABC、△AMN是等邊三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,
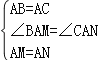
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(2)解:結論∠ABC=∠ACN仍成立;
理由如下:∵△ABC、△AMN是等邊三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,
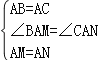
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(3)解:∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,頂角∠ABC=∠AMN,
∴底角∠BAC=∠MAN,
∴△ABC∽△AMN,
∴![]() =
=![]() ,
,
又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】兩名同學進行了10次三級蛙跳測試,經計算,他們的平均成績相同,若要比較這兩名同學的成績哪一位更穩定,通常還需要比較他們成績的( )
A.眾數 B.中位數 C.方差 D.以上都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中,AB為⊙O的直徑,AC是弦,![]() ,
,![]() .
.
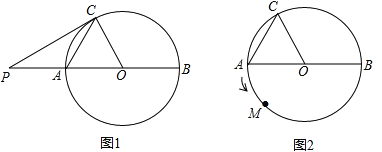
(1)在圖1中,P為直徑BA延長線上的一點,當CP與⊙O相切時,求PO的長;
(2)如圖2,一動點M從A點出發,在⊙O上按逆時針方向運動一周,當![]() 時,求半徑OM所掃過的扇形的面積.
時,求半徑OM所掃過的扇形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2010年3月份,某市市區一周空氣質量報告中某項污染指數的數據是:31,35,31,34,30,32,31,這組數據的中位數、眾數分別是( )
A.32,31 B.31,32 C.31,31 D.32,35
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點A的坐標為(0,1),點C的坐標為(4,3),回答下列問題(直接寫出結果):
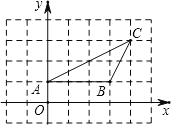
(1)點A關于原點對稱的點的坐標為
(2)點C關于y軸對稱的點的坐標為
(3)若△ABD與△ABC全等,則點D的坐標為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com