
【題目】共享單車作為一種低碳、時尚、綠色的出行方式,它儼然成為市民出行的“新寵”.某公司準備安裝A款共享單車,完成5760輛該款共享單車投入市場運營的計劃.由于抽調不出足夠的熟練工人完成安裝,公司準備招聘一批新工人,將他們培訓到能獨立進行安裝后上崗。生產開始后發現:4名熟練工人和5名新工人每天共安裝88輛共享單車;2名熟練工人每天安裝的共享單車數與3名新工人每天安裝的共享單車數一樣多.
(1)求每名熟練工人和新工人每天分別可以安裝多少輛共享單車?
(2)若公司招聘m名新工人,使得招聘的新工人和抽調的熟練工人剛好一個月(30天)完成安裝任務,已知工人們安裝的共享單車中不能正常投入運營的占4%,且招聘的新工人數比抽調的熟練工人數少,求m的值.
【答案】(1)每名熟練工人每天可以安裝12輛共享單車,新工人每天可以安裝8輛共享單車.(2)1,4,7.
【解析】分析:(1)設每名熟練工每月可以安裝x輛電動車,新工人每月分別安裝y輛電動汽車,根據4名熟練工人和5名新工人每天共安裝88輛共享單車;2名熟練工人每天安裝的共享單車數與3名新工人每天安裝的共享單車數一樣多,兩個等量關系列出方程組,然后求解即可;
(2)設抽調n名熟練工人,根據一年的安裝任務列出方程整理,用m表示出n,然后根據人數m是整數討論求解即可.
詳解:(1)設每名熟練工人每天可以安裝x輛共享單車,新工人每天可以安裝y輛共享單車.
![]() 解得
解得![]()
答:每名熟練工人每天可以安裝12輛共享單車,新工人每天可以安裝8 輛共享單車.
(2)設抽調n名熟練工人(n>m),需安裝5760÷(1-4%)=6000(輛),則(8m+12n)×30=6000 化簡得:2m +3n =50
![]() .∵m、n為正整數且n>m,∴m=1,4,7
.∵m、n為正整數且n>m,∴m=1,4,7


科目:初中數學 來源: 題型:
【題目】某人因需要經常去復印資料,甲復印社按A4紙每10頁2元計費,乙復印社則按A4紙每10頁1元計費,但需按月付一定數額的承包費. 兩復印社每月收費情況如圖所示,根據圖中提供的信息解答下列問題:
(1)乙復印社要求客戶每月支付的承包費是 元.
(2)當每月復印 頁時,兩復印社實際收費相同.
(3)如果每月復印頁在250頁左右時,應選擇哪一個復印社?請簡單說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名大學生去距學校36千米的某鄉鎮進行社會調查.他們從學校出發,騎電動車行駛20分鐘時發現忘帶相機,甲下車前往,乙騎電動車按原路返回.乙取相機后(在學校取相機所用時間忽略不計),騎電動車追甲.在距鄉鎮13.5千米處追上甲后同車前往鄉鎮.乙電動車的速度始終不變.設甲與學校相距y甲(千米),乙與學校相離y乙(千米),甲離開學校的時間為t(分鐘).y甲、y乙與x之間的函數圖象如圖所示,則乙返回到學校時,甲與學校相距________千米.
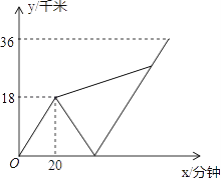
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,矩形OABC的長OA= ![]() ,寬OC=1,將△AOC沿AC翻折得△APC.
,寬OC=1,將△AOC沿AC翻折得△APC.
(1)求∠PCB的度數;
(2)若P,A兩點在拋物線y=﹣ ![]() x2+bx+c上,求b,c的值,并說明點C在此拋物線上;
x2+bx+c上,求b,c的值,并說明點C在此拋物線上;
(3)(2)中的拋物線與矩形OABC邊CB相交于點D,與x軸相交于另外一點E,若點M是x軸上的點,N是y軸上的點,以點E、M、D、N為頂點的四邊形是平行四邊形,試求點M、N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小明坐公交車到濱海公園游玩,他從家出發0.8小時后達到中心書城,逗留一段時間后繼續坐公交車到濱海公園,小明離家一段時間后,爸爸駕車沿相同的路線前往海濱公園. 如圖是他們離家路程s(km)與小明離家時間t(h)的關系圖,請根據圖回答下列問題:
(1)圖中自變量是____,因變量是______;
(2)小明家到濱海公園的路程為____ km,小明在中心書城逗留的時間為____ h;
(3)小明出發______小時后爸爸駕車出發;
(4)圖中A點表示___________________________________;
(5)小明從中心書城到濱海公園的平均速度為______km/h,小明爸爸駕車的平均速度為______km/h;(補充;爸爸駕車經過______追上小明);
(6)小明從家到中心書城時,他離家路程s與坐車時間t之間的關系式為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點D、E、F分別在三邊上,E是AC的中點,AD、BE、CF交于一點G,BD=2DC,S△GEC=3,S△GDC=4,則△ABC的面積是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一座橋如圖,橋下水面寬度AB是20米,高CD是4米.要使高為3米的船通過,則其寬度須不超過多少米. 
(1)如圖1,若把橋看做是拋物線的一部分,建立如圖坐標系. ①求拋物線的解析式; ②要使高為3米的船通過,則其寬度須不超過多少米?
(2)如圖2,若把橋看做是圓的一部分. ①求圓的半徑;②要使高為3米的船通過,則其寬度須不超過多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ΔABC中,以B為圓心,BC長為半徑畫弧,分別交AC、AB于D、E兩點,并連接BD、DE.若∠A=30°,AB=AC,則∠BDE的度數為( )

A. 67.5° B. 52.5° C. 45° D. 75°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com