閱讀快車系列答案科目：初中數學 來源： 題型：
若兩個扇形滿足弧長的比等于它們半徑的比，則這稱這兩個扇形相似。如圖，如果扇形AOB與扇形
是相似扇形，且半徑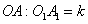
(
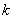為不等于0的常數)。那么下面四個結論：
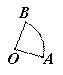
①∠AOB＝∠；②△AOB∽△；③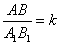
；
④扇形AOB與扇形的面積之比為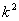
。成立的個數為：
A、1個 B、2個 C、3個 D、4個
查看答案和解析>>
科目：初中數學 來源： 題型：
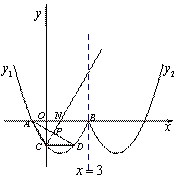
如圖，曲線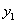
拋物線的一部分，且表達式為：
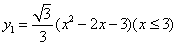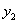曲線
與曲線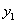關于直線
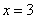對稱。
（1）求A、B、C三點的坐標和曲線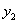的表達式；
（2）過點D作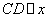
軸交曲線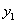于點D，連接AD，在曲線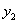上有一點M，使得四邊形ACDM為箏形（如果一個四邊形的一條對角線被另一條對角線垂直平分，這樣的四邊形為箏形），請求出點M的橫坐標。
（3）設直線CM與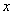
軸交于點N，試問在線段MN下方的曲線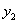上是否存在一點P，使△PMN的面積最大？若存在，求出點P的坐標；若不存在，請說明理由。
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
⊙O為△ABC的外接圓，請僅用無刻度的直尺，根據下列條件分別在圖1，圖2中畫出一條弦，使這條弦將△ABC分成面積相等的兩部分(保留作圖痕跡，不寫作法)．
(1)如圖1，AC＝BC；
(2)如圖2，直線l與⊙O相切與點P，且l∥BC．
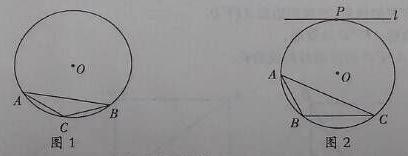
查看答案和解析>>
科目：初中數學 來源： 題型：
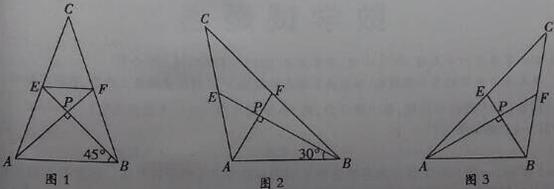
我們把兩條中線互相垂直的三角形稱為“中垂三角形”．例如圖1，圖2，圖3中，AF，BE是△ABC的中線，AF⊥BE，垂足為P，像△ABC這樣的三角形均為“中垂三角形”．設BC＝a，AC＝b，AB＝c．
特例探索
(1)如圖1，當∠ABE＝45°，c＝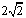
時，a＝ ，b＝ ；
如圖2，當∠ABE＝30°，c＝4時，a＝ ，b＝ ；
歸納證明
(2)請你觀察(1)中的計算結果，猜想a2，b2，c2三者之間的關系，用等式表示出來，請利用圖3證明你發現的關系式；
拓展應用
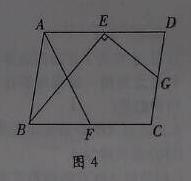
(3)如圖4，在□ABCD中，點E，F，G分別是AD，BC，CD的中點，BE⊥EG，AD＝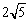
，AB＝3．求AF的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
……，
．
，然后從
的范圍內選取一個合適的整數作為
的值代入求值。