
【題目】如圖,△ABC和△ADE都是等腰直角三角形,CE與BD相交于點M,BD交AC于點N,
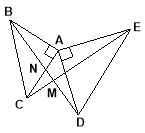
證明:(1)BD=CE. (2)BD⊥CE.
【答案】略
【解析】(1)要證明BD=CE,只要證明△ABD≌△ACE即可,兩三角形中,已知的條件有AD=AE,AB=AC,那么只要再得出兩對應邊的夾角相等即可得出三角形全等的結論.我們發現∠BAD和∠EAC都是90°加上一個∠CAD,因此∠CAE=∠BAD.由此構成了兩三角形全等中的(SAS)因此兩三角形全等.
(2)要證BD⊥CE,只要證明∠BMC是個直角就行了.由(1)得出的全等三角形我們可知:
∠ABN=∠ACE,三角形ABC中,∠ABN+∠CBN+∠BCN=90°,根據上面的相等角,我們可得出∠ACE+∠CBN+∠BCN=90°,即∠ABN+∠ACE=90°,因此∠BMC就是直角了.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
【題目】綜合題
(1)用適當的方法解方程:
①(x﹣2)2=2x﹣4
②x2﹣2x﹣8=0.
(2)先化簡,再求值: ![]() ÷(
÷( ![]() ﹣a+1),其中a是方程x2﹣x=6的根.
﹣a+1),其中a是方程x2﹣x=6的根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是直徑,點D是⊙O上的一點,點C是 ![]() 的中點,弦CM垂直AB于點F,連接AD,交CF于點P,連接BC,∠DAB=30°.
的中點,弦CM垂直AB于點F,連接AD,交CF于點P,連接BC,∠DAB=30°. 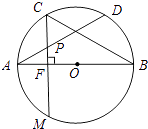
(1)求∠ABC的度數;
(2)若CM=4 ![]() ,求
,求 ![]() 的長度.(結果保留π)
的長度.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀下列材料:
計算:![]() .
.
解法一:原式=
![]()
解法二:原式=(-![]() )÷[(
)÷[(![]() )-(
)-(![]() )]=
)]=![]() ÷
÷![]() =-
=-![]() ×3=-
×3=-![]() .
.
解法三:原式的倒數為(![]() )÷(-
)÷(-![]() )=
)=![]() ×(-30)-
×(-30)-![]() ×(-30)+
×(-30)+![]() ×(-30)-
×(-30)-![]() ×(-30)=-20+3-5+12=-10,
×(-30)=-20+3-5+12=-10,
故原式=-![]() .
.
(1)上述解法得出的結果不同,肯定有錯誤的解法,你認為解法________是錯誤的,在正確的解法中,你認為解法________最簡捷;
(2)利用(1)中你認為最簡捷的解法計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】求兩個正整數的最大公約數是常見的數學問題,中國古代數學專著《九章算術》中便記載了求兩個正整數最大公約數的一種方法——更相減損術,術曰:“可半者半之,不可半者,副置分母、子之數,以少成多,更相減損,求其等也,以等數約之.”意思是說,要求兩個正整數的最大公約數,先用較大的數減去較小的數,得到差,然后用減數與差中的較大數減去較小數,以此類推,當減數與差相等時,此時的差(或減數)即為這兩個正整數的最大公約數.例如:求91與56的最大公約數:
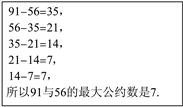
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】東方紅中學位于東西方向的一條路上,一天我們學校的李老師出校門去家訪,他先向西走100米到聰聰家,再向東走150米到青青家,再向西走200米到剛剛家,請問:
(1)如果把這條路看作一條數軸,以向東為正方向,以校門口為原點,請你在這條數軸上標出聰聰家與青青家的大概位置(數軸上一格表示50米).
(2)聰聰家與剛剛家相距多遠?
(3)聰聰家向西20米所表示的數是多少?
(4)你認為可用什么辦法求數軸上兩點之間的距離?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等腰△AOB,AO=AB=5,OB=6.以O為原點,以OB邊所在的直線為x軸,以垂直于OB的直線為y軸建立平面直角坐標系.
(1)求點A的坐標;
(2)若點A關于y軸的對稱點為M,點N的橫、縱坐標之和等于點A的橫坐標,請在圖中畫出一個滿足條件的△AMN,并直接在圖上標出點M,N的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E,F分別是AB,CD上的點,點G是BC的延長線上一點,且∠B=∠DCG=∠D,則下列判斷中,錯誤的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 疊合在一起,邊
疊合在一起,邊 ![]() 與
與 ![]() 重合,
重合, ![]() (如圖1),點
(如圖1),點 ![]() 為邊
為邊 ![]()
![]() 的中點,邊
的中點,邊 ![]() 與
與 ![]() 相交于點
相交于點 ![]() ,此時線段
,此時線段 ![]() 的長是 . 現將三角板
的長是 . 現將三角板 ![]() 繞點
繞點 ![]() 按順時針方向旋轉(如圖2),在
按順時針方向旋轉(如圖2),在 ![]() 從
從 ![]() 到
到 ![]() 的變化過程中,點
的變化過程中,點 ![]() 相應移動的路徑長共為 . (結果保留根號)
相應移動的路徑長共為 . (結果保留根號)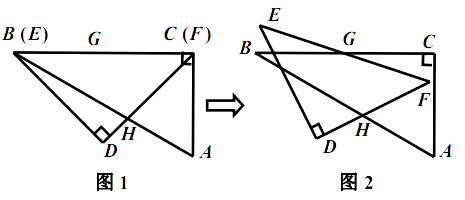
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com