【題目】如圖，在
中，
，
，在
上取一點
，在
上取一點
，使
，過點作
于點
．交
于點
，若
，
，則
的長為________．
【答案】
【解析】
過B作BH⊥BC交DE的延長線于H，則BH∥AC，推出△ADE∽△BHE，根據相似三角形的性質得到
=
，根據平行線的性質得到∠H=∠1，∠2=∠DBH，等量代換得到∠H=∠DBH，于是得到DH=BD，過D作DM⊥BH與M，根據等腰三角形的性質和矩形的性質得到BM=
BH=CD，設CD=x，則BH=2x，根據余角的性質得到∠2=∠3，推出△ADE∽△BFE，根據相似三角形的性質即可得到結論．
過B作BH⊥BC交DE的延長線于H，過D作DM⊥BH與M，則BH∥AC，四邊形DCBM是矩形，∴△ADE∽△BHE，∴=．
∵BH∥AC，∴∠H=∠1，∠2=∠DBH．
∵∠1=∠2，∴∠H=∠DBH，∴DH=BD，∴BM=BH=CD，設CD=x，則BH=2x．
∵EF⊥BD，∴∠BNF=90°，∴∠2+∠CBD=∠3+∠NBF，∴∠2=∠3．
∵∠A=∠FBE=45°，∴∠1=∠3，∴△ADE∽△BFE，∴
==，∴BF=BH，即11+x﹣8=2x，∴x=3，∴CD=3．
故答案為：3．
科目：初中數學 來源： 題型：
【題目】已知，如圖，點B、F、C、E在同一直線上，AC、DF相交于點G，AB⊥BE，垂足為B，DE⊥BE，垂足為E，且AC=DF，BF=EC．求證：
（1）△ABC≌△DEF；
（2）FG=CG．
查看答案和解析>>
科目：初中數學 來源： 題型：
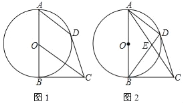
【題目】如圖1，AB是⊙O的直徑，BC是⊙O的切線，OC∥弦AD
（1）求證：CD是⊙O的切線；
（2）如圖2，連AC交BD于E．若AE=CE，求tan∠ACB的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠A＝∠B，AE＝BE，點D在AC邊上，∠1＝∠2，AE和BD相交于點O
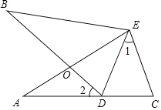
（1）求證：△AEC≌△BED；
（2）若∠1＝38°，求∠BDE的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：
中，
．
求作
邊上的垂直平分線
，使得交于
；將線段
沿著的方向平移到線段
（其中點
平移到點
，畫出平移后的線段；（要求用尺規作圖，不寫作法，保留作圖痕跡．）
連接
、
，試判斷四邊形
是矩形嗎？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知
是等邊三角形，邊
上有一點
，且
、
兩點之間的距離為
.
(1)求的坐標(用含有
的式子表示)；
(2)如圖(1)，若點
在線段
上運動，點
在
軸的正半軸上運動.當
的值最小時，
.
問：的面積是否為定值，若是，求其值；若不是，請說明理由.
(3)如圖(2)，若在外還有一點
，連接
、
、
、
，
，
，求的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知拋物線
過
，
，
三點，點的坐標是
，點的坐標是
，動點
在拋物線上．
________，
________，點的坐標為________；（直接填寫結果）
是否存在點，使得
是以
為直角邊的直角三角形？若存在，求出所有符合條件的點的坐標；若不存在，說明理由；
過動點作
垂直
軸于點
，交直線于點
，過點作
軸的垂線．垂足為
，連接
，當線段的長度最短時，求出點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1, △ABC和△CDE均為等腰三角形，AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a，且點A、D、E在同一直線上，連結BE.
(1)求證: AD=BE.
(2)如圖2,若a=90°，CM⊥AE于E.若CM=7, BE=10, 試求AB的長.
(3)如圖3,若a=120°, CM⊥AE于E, BN⊥AE于N, BN=a, CM=b,直接寫出AE的值(用a, b 的代數式表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
