
【題目】如圖,已知二次函數y=x2-mx-m-1的圖像交x軸于A、B兩點(A、B分別位于坐標原點O的左、右兩側),交y軸于點C,且△ABC的面積為6.
(1)求這個二次函數的表達式;
(2)若P為平面內一點,且PB=3PA,試求當△PAB的面積取得最大值時點P的坐標,并求此時直線PO將△ABC分成的兩部分的面積之比.
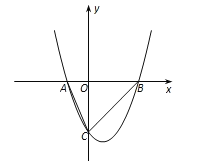
【答案】(1)y=x2-2x-3;(2)5∶3或1∶15.
【解析】
(1)分別求出A,B,C的坐標,結合△ABC的面積為6,列出關于m的方程,求出m的值,即可得到二次函數解析式;
(2)設P(a,b),根據PB=3PA以及兩點間的距離公式,得到b2關于a的二次函數,利用二次函數的性質,求出使△PAB面積最大時,點P的坐標,然后分兩種情況:①當P1(-![]() ,
,![]() )時,②當P2(-
)時,②當P2(-![]() ,-
,-![]() )時,分別求出此時直線PO將△ABC分成的兩部分的面積之比,即可.
)時,分別求出此時直線PO將△ABC分成的兩部分的面積之比,即可.
(1)令y=0,得:0=x2-mx-m-1,解得:x1=-1,x2=m+1,
∴A(-1,0),B(m+1,0).
當x=0時,y=-m-1,
∴C(0,-m-1).
∵B(m+1,0)在y軸的右側,
∴m+1>0,
由“△ABC的面積為6”得:S=![]() (m+1)(m+2)=6,
(m+1)(m+2)=6,
解得:m1=-5(舍去),m2=2,
∴y=x2-2x-3.
(2)設P(a,b),
∵A(-1,0),B(3,0),PB=3PA,
∴PB2=9PA2,即(3-a)2+b2=9[(-1-a)2+b2],
化簡得:b2=-a2-3a.
要使△PAB面積最大,底AB=4為定值,因此只要使AB邊上的高最大,即b2取得最大值.
∵b2=-(a+![]() )2+
)2+![]() ,
,
∴當a=-![]() 時,b2取得最大值為
時,b2取得最大值為![]() ,即
,即![]() 取得最大值為
取得最大值為![]() ,
,
∴P1(-![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
①當P1(-![]() ,
,![]() )時,直線P1O的解析式為:y=-x,
)時,直線P1O的解析式為:y=-x,
∵B(3,0),C(0,-3),
∴直線BC的解析式為:y=x-3.
聯立y=-x與y=x-3,得-x=x-3,解得:x=![]() ,
,
∴P1O與BC的交點Q1(![]() ,-
,-![]() ),
),
∴△OBQ1的面積=![]() ×3×
×3×![]() =
=![]() ,四邊形ACQ1O的面積=6-
,四邊形ACQ1O的面積=6-![]() =
=![]() ,
,
∴此時直線PO將△ABC分成的兩部分的面積之比為![]() ∶
∶![]() ,即5∶3.
,即5∶3.
②當P2(-![]() ,-
,-![]() )時,與①同理可得直線PO將△ABC分成的兩部分的面積之比為1∶15.
)時,與①同理可得直線PO將△ABC分成的兩部分的面積之比為1∶15.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位線,點D在AB上,把點B繞點D按順時針方向旋轉α(0°<α<180°)角得到點F,連接AF,BF.下列結論:①△ABF是直角三角形;②若△ABF和△ABC全等,則α=2∠BAC或2∠ABC;③若α=90°,連接EF,則S△DEF=4.5;其中正確的結論是( )
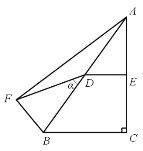
A.①②B.①③C.①②③D.②③
查看答案和解析>>
科目:初中數學 來源: 題型:
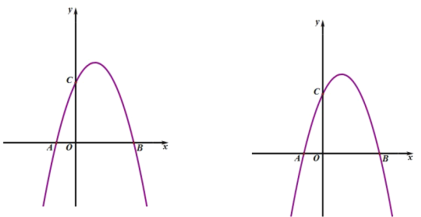
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且
,且![]() .
.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 若點
若點![]() 為第一象限拋物線上一點,連接
為第一象限拋物線上一點,連接![]() ,將線段
,將線段![]() 繞著點
繞著點![]() 逆時針旋轉
逆時針旋轉![]() ,得到線段
,得到線段![]() 連接
連接![]() 過點
過點![]() 作直線
作直線![]() 的垂線,垂足為點E,過點
的垂線,垂足為點E,過點![]() 作直線
作直線![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,作線段
,作線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,求點
,求點![]() 的坐標;
的坐標;
![]() 在
在![]() 的條件下,延長
的條件下,延長![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,當
,當![]() 時,求
時,求![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為平行四邊形ABCD的邊AD上的一點,E,F分別為PB,PC的中點,△PEF,△PDC,△PAB的面積分別為S,![]() ,
,![]() .若S=3,則
.若S=3,則![]() 的值為( )
的值為( )
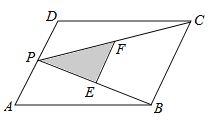
A.24B.12C.6D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形OABC在平面直角坐標系中的位置如圖所示,A、C兩點的坐標分別為A(6,0)、C(0,3),直線![]() 與BC邊相交于點D.
與BC邊相交于點D.

(1)求點D的坐標;
(2)若拋物線![]() 經過A、D兩點,試確定此拋物線的解析式;
經過A、D兩點,試確定此拋物線的解析式;
(3)設(2)中的拋物線的對稱軸與直線AD交于點M,點P為對稱軸上一動點,以P、A、M為頂點的三角形與△ABD相似,求符合條件的所有點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,建筑物BC的屋頂有一根旗桿AB,從地面上點D處觀測旗桿頂點A的仰角為50°,觀測旗桿底部點B的仰角為45°.若旗桿的高度AB為3.5米,則建筑物BC的高度約為_____米.(精確到1米,可用參考數據:sin50°≈0.8,tan50°≈1.2)
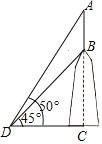
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,以AB為直徑作⊙O,點C是直徑AB上方半圓上的一點,連結AC,BC,過點C作∠ACB的平分線交⊙O于點D,過點D作AB的平行線交CB的延長線于點E.
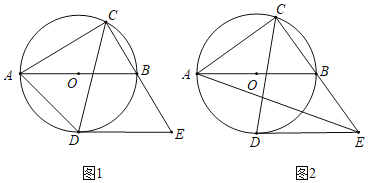
(1)如圖1,連結AD,求證:∠ADC=∠DEC.
(2)若⊙O的半徑為5,求CACE的最大值.
(3)如圖2,連結AE,設tan∠ABC=x,tan∠AEC=y,
①求y關于x的函數解析式;
②若![]() =
=![]() ,求y的值.
,求y的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明研究一函數的性質,下表是該函數的幾組對應值:
| ··· | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ···· |
| ··· | 8 | 3 | 0 | -1 | 0 | 3 | 0 | -3 | -6 | ···· |
![]() 在平面直角坐標系中,描出以上表格中的各點,根據描出的點,畫出該函數圖象
在平面直角坐標系中,描出以上表格中的各點,根據描出的點,畫出該函數圖象
![]() 根據所畫函數圖象,寫出該函數的一條性質: ;
根據所畫函數圖象,寫出該函數的一條性質: ;
![]() 根據圖像直接寫出該函數的解析式及自變量的取值范圍: ;
根據圖像直接寫出該函數的解析式及自變量的取值范圍: ;
![]() 若一次函數
若一次函數![]() 與該函數圖像有三個交點,則
與該函數圖像有三個交點,則![]() 的范圍是
的范圍是

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】西安市某學校在“我們如何預防感染新型冠狀病毒”宣講培訓后,對學生知曉情況進行了一次測試,其測試成績按照標準劃分為四個等級:![]() 優秀,
優秀,![]() 良好,
良好,![]() 合格,
合格,![]() 不合格.為了了解該校學生的成績狀況,對在校學生進行隨機抽樣調查,并對調查結果進行統計,如圖所示.
不合格.為了了解該校學生的成績狀況,對在校學生進行隨機抽樣調查,并對調查結果進行統計,如圖所示.
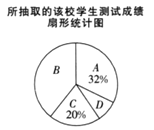

請結合統計圖回答下列問題:
(1)該校抽樣調查的學生人數為___________.
(2)請補全條形統計圖.
(3)樣本中,學生成績的中位數所在等級是______.(填“![]() ”、“
”、“![]() ”、“
”、“![]() ”或“
”或“![]() ”)
”)
(4)該校共有學生2500人,估計全校測試成績為優秀和良好的學生共有______人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com