
【題目】嘉嘉和琪琪在用一副三角尺研究數學問題:
一副三角尺分別有一個角為直角,其余角度如圖1所示,![]() .
.
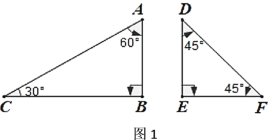
發現:
(1)如圖2,當![]() 與
與![]() 重合時,
重合時,![]() _____.
_____.
(2)如圖3,將圖2中![]() 繞
繞![]() 點順時針旋轉一定角度使得
點順時針旋轉一定角度使得![]() ,求
,求![]() 的度數.
的度數.
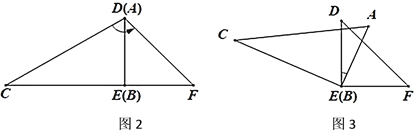
拓展:
(3)如圖4,繼續旋轉,使得![]() 于點
于點![]() ,
,
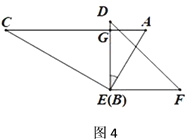
①此時![]() 與
與![]() 平行嗎?請說明理由.
平行嗎?請說明理由.
②求![]() 的度數.
的度數.
探究:
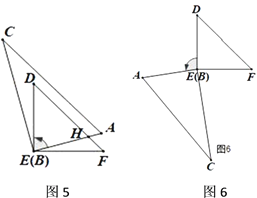
(4)如圖5、圖6,繼續旋轉,使得![]() ,求
,求![]() 的度數.
的度數.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①平行,垂直于同一條直線的兩條直線平行;②
;(3)①平行,垂直于同一條直線的兩條直線平行;②![]() ;(4)
;(4)![]() ,
,![]() ;
;
【解析】
(1)利用角的和差關系計算即可;(2)利用角的和差關系計算即可;(3)①根據平行線的判定定理即可得答案;②利用直角三角形兩銳角互余的性質即可得答案;(4)在圖5中,根據平行線的性質可得∠DHE的度數,根據三角形內角和定理即可求出∠AED的度數,在圖6中,過E作EG//AC,根據平行線的性質即可得∠AED的度數.
(1)∵∠CAB=60°,∠EDF=45°,
∴∠CDF=∠CAB+∠EDF=105°,
(2)∵![]() ,∠CBA=90°,∠DEF=90°,
,∠CBA=90°,∠DEF=90°,
∴∠CBA+∠AEB=∠CBA+∠DEF-∠AED=90°+90°-∠AED=156°,
∴∠AED=180°-156°=24°.
(3)①平行,理由如下:
∵![]() ,∠DEF=90°,
,∠DEF=90°,
∴AC//EF.
②∵![]() ,∠C=30°,
,∠C=30°,
∴∠CED=90°-30°=60°,
∵∠CBA=90°,
∴∠AED=90°-60°=30°,
(4)在圖5中,
∵AC//EF,
∴∠DHE=∠A=60°,
∵∠D=45°,
∴∠AED=180°-60°-45°=75°,
在圖6中,過過E作EG//AC,
∵AC//DF,EG//AC,
∴EG//DF,
∴∠DEG=∠D=45°,∠AEG=∠A=60°,
∴∠AED=45°+60°=105°,


科目:初中數學 來源: 題型:
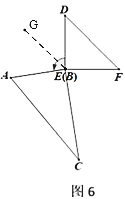
【題目】問題情境:如圖1,AB∥CD,∠A=30°,∠C=40°,求∠AEC的度數.小明的思路是:

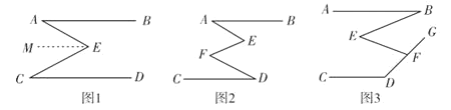
(1)初步嘗試:按小明的思路,求得∠AEC的度數;
(2)問題遷移:如圖2,AB∥CD,點E、F為AB、CD內部兩點,問∠A、∠E、∠F和∠D之間有何數量關系?請說明理由;
(3)應用拓展:如圖3,AB∥CD,點E、F為AB、CD內部兩點,如果∠E+∠EFG=160°,請直接寫出∠B與∠D之問的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是等邊三角形,D是BC邊上的一個動點
是等邊三角形,D是BC邊上的一個動點![]() 點D不與B,C重合
點D不與B,C重合![]() 是以AD為邊的等邊三角形,過點F作BC的平行線交射線AC于點E,連接BF.
是以AD為邊的等邊三角形,過點F作BC的平行線交射線AC于點E,連接BF.
![]() 如圖1,求證:
如圖1,求證:![]() ≌
≌![]() ;
;
![]() 請判斷圖1中四邊形BCEF的形狀,并說明理由;
請判斷圖1中四邊形BCEF的形狀,并說明理由;
![]() 若D點在BC邊的延長線上,如圖2,其它條件不變,請問
若D點在BC邊的延長線上,如圖2,其它條件不變,請問![]() 中結論還成立嗎?如果成立,請說明理由.
中結論還成立嗎?如果成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業前年按可回收垃圾處理費15元/噸、不可回收垃圾處理費25元/噸的收費標準,共支付兩種垃圾處理費5000元,從去年元月起,收費標準上調為:可回收垃圾處理費30元/噸,不可回收垃圾處理費100元/噸.若該企業去年處理的這兩種垃圾數量與前年相比沒有變化,但調價后就要多支付處理費9000元.
(1)該企業前年處理的可回收垃圾和不可回收垃圾各多少噸?
(2)該企業計劃今年將上述兩種垃圾處理總量減少到200噸,且可回收垃圾不少于不可回收垃圾處理量的3倍,則今年該企業至少有多少噸可回收垃圾?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】世界上大部分國家都使用攝氏溫度(![]() ),但美國、英國等國家的天氣預報仍然使用華氏溫度(
),但美國、英國等國家的天氣預報仍然使用華氏溫度(![]() ).兩種計量之間有如下對應:
).兩種計量之間有如下對應:
攝氏溫度( |
|
|
|
|
|
|
華氏溫度( |
|
|
|
|
|
|
(1)上表反映了哪兩變量之間的關系?哪個是自變量?哪個是因變量?
(2)由上表可得:攝氏溫度(![]() )每提高
)每提高![]() 度,華氏溫度(
度,華氏溫度(![]() )提高_____度.
)提高_____度.
(3)攝氏溫度![]() 度時華氏溫度為______度.
度時華氏溫度為______度.
(4)華氏溫度![]() 度時攝氏溫度為_______度.
度時攝氏溫度為_______度.
(5)華氏溫度的值與對應的攝氏溫度的值有相等的可能嗎?如果有,求出這個值.如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地震救援隊探測出某建筑物廢墟下方點C處有生命跡象,已知廢墟一側地面上兩探測點A,B相距3米,探測線與地面的夾角分別是30°和60°(如圖),試確定生命所在點C的深度.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為開展全科大閱讀活動,學校花費了3400元在書店購買了40套古典文學書籍和20套現代文學書籍,每套現代文學書籍比每套古典文學書籍多花20元.
(1)求每套古典文學習書籍和現代文學書籍分別是多少元?
(2)為滿足學生的閱讀需求,學校計劃用不超過2500元再次購買古典文學和現代文學書籍共40套,經市場調查得知,每套古典文學書籍價格上浮了20%,每套現代文學書籍價格下調了10%,學校最多能購買多少套現代文學書籍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題再現:
數形結合是一種重要的數學思想方法,借助這種思想方法可將抽象的數學知識變得直觀并且具有可操作性.初中數學里的一些代數公式,很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.
例如:利用圖形的幾何意義驗證完全平方公式.
將一個邊長為![]() 的正方形的邊長增加
的正方形的邊長增加![]() ,形成兩個長方形和兩個正方形,如圖所示:這個圖形的面積可以表示成:
,形成兩個長方形和兩個正方形,如圖所示:這個圖形的面積可以表示成:
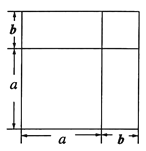
![]() 或
或![]()
∴![]()
這就驗證了兩數和的完全平方公式.
類比解決:
請你類比上述方法,利用圖形的幾何意義驗證平方差公式.
(要求畫出圖形并寫出推理過程)
問題提出:如何利用圖形幾何意義的方法證明![]() ?
?
如圖所示,![]() 表示1個1×1的正方形,即:
表示1個1×1的正方形,即:![]() ,
,![]() 表示1個2×2的正方形,
表示1個2×2的正方形,![]() 與
與![]() 恰好可以拼成1個2×2的正方形,因此:
恰好可以拼成1個2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2個2×2的正方形,即:
就可以表示2個2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一個
恰好可以拼成一個![]() 的大正方形.
的大正方形.
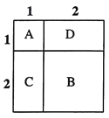
由此可得:![]() .
.
嘗試解決:
請你類比上述推導過程,利用圖形的幾何意義確定:![]() _______.(要求寫出結論并構造圖形寫出推證過程).
_______.(要求寫出結論并構造圖形寫出推證過程).
問題拓廣:
請用上面的表示幾何圖形面積的方法探究:![]() _______.(直接寫出結論即可,不必寫出解題過程).
_______.(直接寫出結論即可,不必寫出解題過程).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com