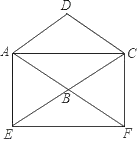
【題目】已知：如圖，菱形ABCD，分別延長AB，CB到點F，E，使得BF=BA，BE=BC，連接AE，EF，FC，CA．
（1）求證：四邊形AEFC為矩形；
（2）連接DE交AB于點O，如果DE⊥AB，AB=4，求DE的長．
【答案】（1）證明見解析；（2）ED=4
．.
【解析】
（1）根據菱形的性質以及矩形的判定證明即可；
（2）連接DB，根據菱形的判定和性質以及直角三角形的性質解答即可．
（1）證明：∵BF=BA，BE=BC，
∴四邊形AEFC為平行四邊形，
∵四邊形ABCD為菱形，
∴BA=BC，
∴BE=BF，
∴BA+BF=BC+BE，即AF=EC，
∴四邊形AEFC為矩形；
（2）連接DB，
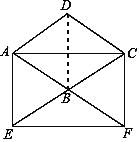
由（1）可知，AD∥EB，且AD=EB，
∴四邊形AEBD為平行四邊形，
∵DE⊥AB，
∴四邊形AEBD為菱形，
∴AE=EB，AB=2AG，ED=2EG，
∵矩形ABCD中，EB=AB，AB=4，
∴AG=2，AE=4，
∴在Rt△AEG中，EG=2，
∴ED=4．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，點M在CD邊上，點N在正方形ABCD外部，且滿足∠CMN＝90°，CM＝MN．連接AN，CN，取AN的中點E，連接BE，AC，交于F點．
（1） ①依題意補全圖形；②求證：BE⊥AC．
（2）設AB＝1，若點M沿著線段CD從點C運動到點D，則在該運動過程中，線段EN所掃過的面積為 （直接寫出答案）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，D、E、F分別為AB、BC、AC的中點，則下列結論：①△ADF≌△FEC；②四邊形ADEF為菱形；③
。其中正確的結論是____________.（填寫所有正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
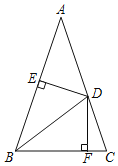
【題目】如圖，△ABC中，AB＝AC，∠A＝36°，D是AC上一點，且BD＝BC，過點D分別作DE⊥AB，DF⊥BC，垂足分別是E，F，下列結論：①BD是∠ABC的平分線；②D是AC的中點；③DE垂直平分AB；④AB＝BC+CD；其中正確的結論是_____（填序號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
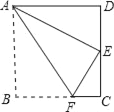
【題目】如圖，四邊形ABCD為平行四邊形紙片．把紙片ABCD折疊，使點B恰好落在CD邊上，折痕為AF．且AB=10cm、AD=8cm、DE=6cm．
（1）求證：平行四邊形ABCD是矩形；
（2）求BF的長；
（3）求折痕AF長．
查看答案和解析>>
科目：初中數學 來源： 題型：
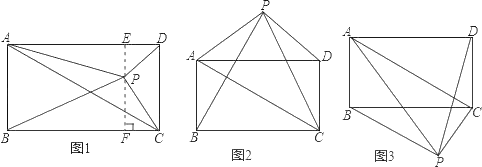
【題目】已知矩形ABCD和點P，當點P在圖1中的位置時，則有結論：S△PBC=S△PAC+S△PCD
理由：過點P作EF垂直BC，分別交AD、BC于E、F兩點．
∵S△PBC+S△PAD=
BCPF+ADPE=BC（PF+PE）=BCEF=S矩形ABCD．
（1）請補全以上證明過程．
（2）請你參考上述信息，當點P分別在圖1、圖2中的位置時，S△PBC、S△PAC、SPCD又有怎樣的數量關系？請寫出你對上述兩種情況的猜想，并選擇其中一種情況的猜想給予證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知在△ABC中，CD⊥AB于點D，BD＝9，BC＝15，AC＝20.
(1)求CD的長；
(2)求AB的長；
(3)判斷△ABC的形狀．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在下列命題中，是假命題的個數有（ ）
①如果
，那么
. ② 兩條直線被第三條直線所截，同位角相等
③面積相等的兩個三角形全等 ④ 三角形的一個外角等于不相鄰的兩個內角的和.
A.3個B.2個C.1個D.0個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，點D是AB的中點，連結CD，過點B作BG⊥CE，分別交CD、CA于點E、F，與過點A且垂直于AB的直線相交于點G，連結DF．給出以下五個結論：
①
；②
；③點F是GE的中點；④
；⑤
，其中正確結論的個數是（ ）
A. 
B. 
C. 
D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com