
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發,沿著
出發,沿著![]() 的三條邊逆時針走一圈回到
的三條邊逆時針走一圈回到![]() 點,速度為2
點,速度為2![]() ,設運動時間為
,設運動時間為![]() 秒.
秒.
(1)![]() 時,
時,![]() 為等腰三角形?
為等腰三角形?
(2)另有一點![]() 從點
從點![]() 開始,按順時針走一圈回到
開始,按順時針走一圈回到![]() 點,且速度為每秒3cm,若
點,且速度為每秒3cm,若![]() 、
、![]() 兩點同時出發,當
兩點同時出發,當![]() 、
、![]() 中有一點到達終點時,另一點也停止運動.當
中有一點到達終點時,另一點也停止運動.當![]() 為何值時,直線
為何值時,直線![]() 把
把![]() 的周長分成相等的兩部分?
的周長分成相等的兩部分?

【答案】(1)t=8或6.5;(2)t=2.4或7.2
【解析】
(1)分情況討論:①在邊AB上時,有兩種情況;②在邊AB上時,不能構成三角形;③在邊AC上時,不能構成三角形;
(2)分情況討論:根據點P在BC、AB、AC邊上討論,根據周長平分列方程可得結論.
(1)①i當點P在AB上,如圖,
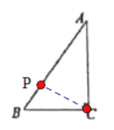
CA=AP時,AP=8,
則t=16÷2=8s,
①ii當點P在AB上,如圖,
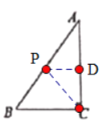
AP=CP時,過P作PD⊥AC于D,則AD=CD=![]() AC=4
AC=4
根據![]()
∴![]()
∴![]()
∴在Rt△PAC中,AP=![]() =5
=5
則t=13÷2=6.5s
故當t=8或6.5秒時,△ACP為等腰三角形;
(2)當P點在AC上,Q在AB上,PQ是相背運動,根據平分周長,則PQ運動的距離和是12,
∵直線PQ把△ABC的周長分成相等的兩部分,
∴2t+3t=12,
∴t=2.4;
當P點在AB上,Q在AC上,相遇后是剛剛好合計走完一周,再次平分時又合計走了半周,
∵直線PQ把△ABC的周長分成相等的兩部分,
∴2t+3t=36,
∴t=7.2,
∴當t=2.4或7.2秒時,直線PQ把△ABC的周長分成相等的兩部分.


科目:初中數學 來源: 題型:
【題目】學生的學業負擔過重會嚴重影響學生對待學習的態度.為此我市教育部門對部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計我市近8000名八年級學生中大約有多少名學生學習態度達標(達標包括A級和B級)?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,AB=AC,AD=AE,BE與CD相交于點P.

(1)求證:PC=PB;
(2)求證:∠CAP=∠BAP;
(3)利用(2)的結論,用直尺和圓規作∠MON的平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
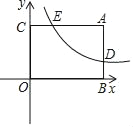
【題目】如圖所示,已知矩形ABOC中,AC=4,雙曲線y=![]() 與矩形兩邊AB、AC分別交于D、E,E為AC邊中點.
與矩形兩邊AB、AC分別交于D、E,E為AC邊中點.
(1)求點E的坐標;
(2)點P是線段OB上的一個動點,是否存在點P,使∠DPC=90°?若存在,求出此時點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的周長是20 cm,以AB,AD為邊向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面積之和為68 cm2,那么矩形ABCD的面積是_______cm2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方體的長為15寬為10,高為20,點B離點C的距離為5,一只螞蟻如果要沿著長方體的表面從點A爬到點B,需要爬行的最短距離是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,點D為△ABC外一點,DC與AB交于點O,且∠BDC=∠BAC.

(1)求證:∠ABD=∠ACD;
(2)過點A作AM⊥CD于M,求證:BD+DM=CM.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某班數學興趣小組利用數學知識測量建筑物DEFC的高度.他們從點A出發沿著坡度為i=1:2.4的斜坡AB步行26米到達點B處,此時測得建筑物頂端C的仰角α=35°,建筑物底端D的俯角β=30°.若AD為水平的地面,則此建筑物的高度CD約為( )米.(參考數據:![]() ≈1.7,tan35°≈0.7)
≈1.7,tan35°≈0.7)

A. 23.1 B. 21.9 C. 27.5 D. 30
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com