
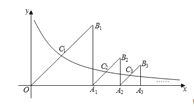
【題目】如圖,△OA1B1,△A1A2B2,△A2A3B3,…是分別以A1,A2,A3,…為直角頂點,一條直角邊在x軸正半軸上的等腰直角三角形,其斜邊的中點C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函數y![]() (x>0)的圖象上.則y1+y2+…+y20的值為____.
(x>0)的圖象上.則y1+y2+…+y20的值為____.
【答案】![]()
【解析】
根據反比例函數關系式及等腰直角三角形的性質,求出點C1的坐標,確定y1,由點C1是等腰直角三角形的斜邊中點,可以得到OA1的長,然后再設未知數,表示點C2的坐標,確定y2,代入反比例函數的關系式,建立方程解出未知數,表示點C3的坐標,確定y3,……然后再求和.
解:過點C1,C2,C3,…分別作x軸的垂線,垂足分別為D1,D2,D3,…
則∠OD1C1=∠OD2C2=∠OD3C3=90°,
∵△OA1B1是等腰直角三角形,
∴∠A1OB1=45°,
∴∠OC1D1=45°,
∴D1C1= OD1,
∵點C1在反比例函數y![]() 上,
上,
∴C1(2,2)
即y1=2,
∴OD1=D1A1=2,
∴OA1=2OD1=4,
設A1D2=a(a>0)則C2D2=a,此時C2(4+a,a),代入y![]() 上得:
上得:
![]() ,解得:
,解得:![]() (舍去),
(舍去),
即![]()
同理:![]()
![]()
……
∴y1+y2+…+y20=![]() ,
,
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】 鄭州某商場在“六一”兒童節購進一批兒童智力玩具.已知成批購進時單價20元,調查發現:該玩具的月銷售量y(個)與銷售單價x(元)之間滿足一次函數關系,下表是月銷售量、銷售單價的幾組對應關系:
月銷售單價x/元 | 30 | 35 | 40 | 45 |
月銷售量y/個 | 230 | 180 | 130 | m |
(1)求y與x的函數關系式;
(2)根據以上信息填空:
①m=______;
②當銷售單價x=______元時,月銷售利潤最大,最大利潤是______元;
(3)根據物價部門規定,每件玩具售價不能高于40元,若月銷售利潤不低于2520元,試求銷售單價x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AB為半圓O的直徑,半徑的長為4cm,點C為半圓上一動點,過點C作CE⊥AB,垂足為點E,點D為弧AC的中點,連接DE,如果DE=2OE,求線段AE的長.
小何根據學習函數的經驗,將此問題轉化為函數問題解決.
小華假設AE的長度為xcm,線段DE的長度為ycm.
(當點C與點A重合時,AE的長度為0cm),對函數y隨自變量x的變化而變化的規律進行探究.
下面是小何的探究過程,請補充完整:(說明:相關數據保留一位小數).
(1)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 |
| 5.8 | 5.7 |
當x=6cm時,請你在圖中幫助小何完成作圖,并使用刻度尺度量此時線段DE的長度,填寫在表格空白處:
(2)在圖2中建立平面直角坐標系,描出補全后的表中各組對應值為坐標的點,畫出該函數的圖象;
(3)結合畫出的函數圖象解決問題,當DE=2OE時,AE的長度約為 cm.
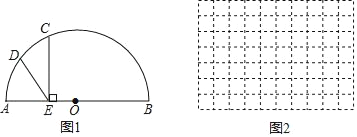
查看答案和解析>>
科目:初中數學 來源: 題型:
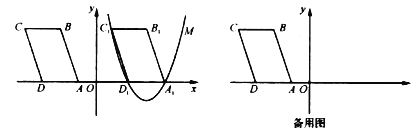
【題目】如圖,在平面直角坐標系![]() 中,已知點
中,已知點![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 是平行四邊形.現將
是平行四邊形.現將![]() 沿
沿![]() 軸方向平移
軸方向平移![]() 個單位,得到
個單位,得到![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,
,![]() ,
,![]() .
.
(1)若拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,求拋物線
,求拋物線![]() 的解析式;
的解析式;
(2)拋物線![]() 的頂點為
的頂點為![]() ,若以
,若以![]() ,
,![]() ,
,![]() 為頂點的三角形的面積等于
為頂點的三角形的面積等于![]() 的面積的一半,求
的面積的一半,求![]() 的值;
的值;
(3)在(2)的條件下,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() ?若存在,請直接寫出點
?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求解方程:
(1)直接開平方法: 4(t-3)2=9(2t-3)2
(2)配方法:2x2-7x-4=0
(3)公式法: 3x2+5(2x+1)=0
(4)因式分解法:3(x-5)2=2(5-x)
(5)abx2-(a2+b2)x+ab=0 (ab≠0)
(6)用配方法求最值:6x2-x-12
查看答案和解析>>
科目:初中數學 來源: 題型:
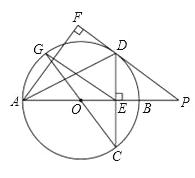
【題目】如圖,已知⊙O半徑為3,直徑AB垂直弦CD于E,過點A作∠DAF=∠DAB,過點D作AF的垂線,垂足為點F,交AB的延長線于點P,連接CO并延長與圓交于點G,連接EG.
(1)求證:DF是⊙O的切線;
(2)若AD=DP,求![]() 的長度;
的長度;
(3)若tanC![]() ,求線段EG的長.
,求線段EG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為H,連接AC,過![]() 上一點E作EG∥AC交CD的延長線于點G,連接AE交CD于點F,且EG=FG.
上一點E作EG∥AC交CD的延長線于點G,連接AE交CD于點F,且EG=FG.
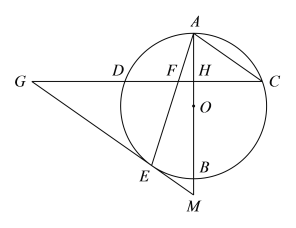
(1)求證:EG是⊙O的切線;
(2)延長AB交GE的延長線于點M,若AH=2,![]() ,求OM的長.
,求OM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年,西安被稱為“網紅城市”.某公司為了讓員工了解騰飛的大西安,感受西安厚重的人文情懷和悠久的歷史,組織員工到西安旅游.這個公司聯系了甲、乙兩家旅行社,他們的報價均為 280 元/人.若參觀人數不超過 10 人,均無優惠;若參觀人數超過 10 人,甲旅行社將超出人員的費用按報價打八折,而乙旅行社將全體參觀人員的費用按報價打九折.現在該公司結合實際情況,想從甲、乙兩家旅行社中選取一家承擔這項參觀業務.設該公司參觀世園的人數為 x(x>10),甲、乙兩家旅行社收取的費用分別為 y1(元)和 y2(元).
(1)分別求出 y1 和 y2 與 x 之間的函數關系式;
(2)假設兩家旅行社除優惠方案不同外,其他服務基本相同.請問該公司選擇哪家旅行社費用較低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com