
【題目】如圖直線![]() 對應的函數表達式為
對應的函數表達式為![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() .直線
.直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,且經過點
,且經過點![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
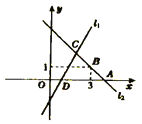
(1)求點![]() ,點
,點![]() 的坐標;
的坐標;
(2)求直線![]() 對應的函數表達式;
對應的函數表達式;
(3)求![]() 的面積;
的面積;
(4)利用函數圖象寫出關于![]() ,
,![]() 的二元一次方程組
的二元一次方程組![]() 的解.
的解.
【答案】(1)點D的坐標為(1,0),點C的坐標為(2,2);(2)![]() ;(3)3;(4)
;(3)3;(4)![]()
【解析】
(1)將y=0代入直線![]() 對應的函數表達式中即可求出點D的坐標,將點
對應的函數表達式中即可求出點D的坐標,將點![]() 代入直線
代入直線![]() 對應的函數表達式中即可求出點C的坐標;
對應的函數表達式中即可求出點C的坐標;
(2)根據圖象可知點B的坐標,然后將點B和點C的坐標代入![]() 中,即可求出直線
中,即可求出直線![]() 對應的函數表達式;
對應的函數表達式;
(3)過點C作CE⊥x軸,先求出點A的坐標,然后根據三角形的面積公式求面積即可;
(4)根據二元一次方程組的解和兩個一次函數交點坐標關系即可得出結論.
解:(1)將y=0代入![]() 中,解得x=1
中,解得x=1
∴點D的坐標為(1,0)
將點![]() 代入
代入![]() 中,得
中,得
![]()
解得:![]()
∴點C的坐標為(2,2);
(2)由圖象可知:點B的坐標為(3,1)
將點B和點C的坐標代入![]() 中,得
中,得
![]()
解得:![]()
∴直線![]() 對應的函數表達式為
對應的函數表達式為![]() ;
;
(3)過點C作CE⊥x軸于E,

將y=0代入![]() 中,解得x=4
中,解得x=4
∴點A的坐標為(4,0)
∵點D(1,0),點C(2,2)
∴AD=4-1=3,CE=2
∴S△ADC=![]() ;
;
(4)∵直線![]() ,
,![]() 交于點
交于點![]()
∴關于![]() ,
,![]() 的二元一次方程組
的二元一次方程組![]() 的解為
的解為![]() .
.


科目:初中數學 來源: 題型:
【題目】根據《居民家庭親子閱讀消費調查報告》中的相關數據制成扇形統計圖,由圖可知,下列說法錯誤的是( )

A.扇形統計圖能反映各部分在總體中所占的百分比
B.每天閱讀30分鐘以上的居民家庭孩子超過50%
C.每天閱讀1小時以上的居民家庭孩子占20%
D.每天閱讀30分鐘至1小時的居民家庭孩子對應扇形的圓心角是108°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形AOBC中,對角線交于點E,雙曲線y=![]() (k>0)經過A、E兩點,若AC : OB = 1:3,梯形AOBC面積為24,則k =( )
(k>0)經過A、E兩點,若AC : OB = 1:3,梯形AOBC面積為24,則k =( )
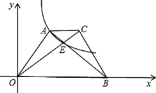
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
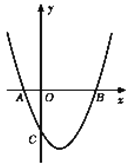
【題目】如圖,拋物線![]() 與x軸交于A、B兩點,與y軸交于點C(0,
與x軸交于A、B兩點,與y軸交于點C(0,![]() ).
).
(1)![]() _____,點A的坐標為______,點B的坐標為_____;
_____,點A的坐標為______,點B的坐標為_____;
(2)設拋物線![]() 的頂點為M,求四邊形ABMC的面積;
的頂點為M,求四邊形ABMC的面積;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校運動會需購買A,B兩種獎品,若購買A種獎品3件和B種獎品2件,共需60元;若購買A種獎品5件和B種獎品3件,共需95元.
(1)求A、B兩種獎品的單價各是多少元?
(2)學校計劃購買A、B兩種獎品共100件,購買費用不超過1150元,且A種獎品的數量不大于B種獎品數量的3倍,設購買A種獎品m件,購買費用為W元,寫出W(元)與m(件)之間的函數關系式.求出自變量m的取值范圍,并確定最少費用W的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,二次函數y=﹣2x2+4x+m的圖象與x軸的一個交點為A(3,0),另一個交點為B,且與y軸交于點C.
(1)求m的值及點B的坐標;
(2)求△ABC的面積;
(3)該二次函數圖象上有一點D(x,y),使S△ABD=S△ABC,請求出D點的坐標.
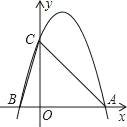
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①c<0;②2a+b=0;③a+b+c<0;④b2-4ac<0,其中正確的有( )
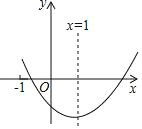
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com