
【題目】如圖,將ABCD沿EF對折,使點A落在點C處,若∠A=60°,AD=4,AB=8,則AE的長為__.

【答案】![]()
【解析】
過點C作CG⊥AB的延長線于點G,易證△D′CF≌△ECB(ASA),從而可知D′F=EB,CF=CE,設AE=x,在△CEG中,利用勾股定理列出方程即可求出x的值.
過點C作CG⊥AB的延長線于點G,
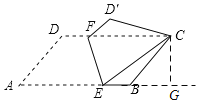
在ABCD中,∠D=∠EBC,AD=BC,∠A=∠DCB,
由于ABCD沿EF對折,
∴∠D′=∠D=∠EBC,∠D′CE=∠A=∠DCB,
D′C=AD=BC,
∴∠D′CF+∠FCE=∠FCE+∠ECB,
∴∠D′CF=∠ECB,且∠D'=∠EBC,D'C=BC
∴△D′CF≌△ECB(ASA)
∴D′F=EB,CF=CE,
∵DF=D′F,
∴DF=EB,AE=CF
設AE=x,則EB=8﹣x,CF=x,
∵BC=4,∠CBG=60°,
∴BG=![]() BC=2,
BC=2,
在Rt△BCG中,由勾股定理可知:CG=![]() ,
,
∴EG=EB+BG=8﹣x+2=10﹣x
在Rt△CEG中,由勾股定理可知:(10﹣x)2+(2![]() )2=x2,
)2=x2,
∴x=![]()
∴AE=![]()
故答案為:![]()


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】 小明遇到這樣一個問題
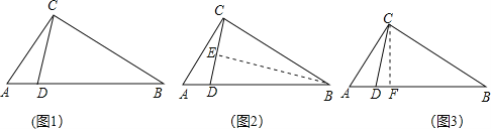
如圖1,△ABC中,∠ACB=90°,點D在AB上,且BD=BC,求證:∠ABC=2∠ACD.
小明發現,除了直接用角度計算的方法外,還可以用下面兩種方法:
方法2:如圖2,作BE⊥CD,垂足為點E.
方法3:如圖3,作CF⊥AB,垂足為點F.
根據閱讀材料,從三種方法中任選一種方法,證明∠ABC=2∠ACD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次籃球比賽中,如圖隊員甲正在投籃.已知球出手時離地面![]() m,與籃圈中心的水平距離為7 m,球出手后水平距離為4 m時達到最大高度4 m,設籃球運行軌跡為拋物線,籃圈距地面3 m.
m,與籃圈中心的水平距離為7 m,球出手后水平距離為4 m時達到最大高度4 m,設籃球運行軌跡為拋物線,籃圈距地面3 m.
(1)建立如圖所示的平面直角坐標系,問此球能否準確投中?
(2)此時,對方隊員乙在甲面前1 m處跳起蓋帽攔截,已知乙的最大摸高為3.1 m,那么他能否獲得成功?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.阜陽市某家快遞公司,2017年3月份與5月份完成投遞的快遞總件數分別為10萬件和12.1萬件.現假定該公司每月投遞的快遞總件數的增長率相同.
(1)求該快遞公司投遞快遞總件數的月平均增長率?
(2) 如果平均每人每月最多可投遞快遞0.6萬件,那么該公司現有的21名快遞投遞業務員能否完成2017年6月份的快遞投遞任務?如果不能,請問至少需要增加幾名業務員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗探究:
(1)如圖1,對折矩形紙片ABCD,使AD與BC重合,得到折痕EF,把紙片展開;再一次折疊紙片,使點A落在EF上,并使折痕經過點B,得到折痕BM,同時得到線段BN,MN.請你觀察圖1,猜想∠MBN的度數是多少,并證明你的結論.
(2)將圖1中的三角形紙片BMN剪下,如圖2,折疊該紙片,探究MN與BM的數量關系,寫出折疊方案,并結合方案證明你的結論.
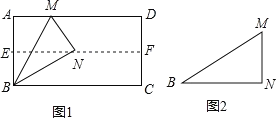
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,O為坐標原點,A(1,1),在x軸上確定點P,使△AOP為等腰三角形,則符合條件的點P的個數共有( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)解方程x2﹣4x=12;
(2)如圖,△ABP是由△ACE繞A點旋轉得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋轉角的度數.
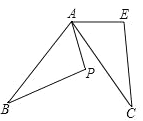
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com