
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 是
是![]() 上一點,且
上一點,且![]() 平分
平分![]() ,點
,點![]() 是
是![]() 上一點,以
上一點,以![]() 為直徑的
為直徑的![]() 經過點
經過點![]() .
.
![]() 求證:
求證:![]() 是
是![]() 的切線;
的切線;
![]() 若
若![]() 的面積
的面積![]() 的面積
的面積![]() ,
,![]() ,求
,求![]() 的長.
的長.
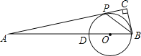
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)連結OP,如圖,由BP平分∠ABC得∠CBP=∠OBP,由OB=OP得∠OBP=∠OPB,則∠CBP=∠OPB,根據平行線的判定得OP∥BC,則利用平行線的性質得到∠APO=∠C=90°,于是可根據切線的判定定理得到結論;
(2)根據三角形面積公式由△ABP的面積-△BPC的面積=2可得BC(PA-1)=4,即BC=![]() ,再根據平行線分線段成比例定理可推出
,再根據平行線分線段成比例定理可推出![]() ,則AB=PABC,接著利用勾股定理有AB2=AC2+BC2,所以PA2BC2=(AP+1)2+BC2,移項變形得到(AP+1)2=BC2(PA2-1),所以PA+1=BC2(PA-1),然后把BC=
,則AB=PABC,接著利用勾股定理有AB2=AC2+BC2,所以PA2BC2=(AP+1)2+BC2,移項變形得到(AP+1)2=BC2(PA2-1),所以PA+1=BC2(PA-1),然后把BC=![]() 代入得到關于PA的方程,然后解方程即可.
代入得到關于PA的方程,然后解方程即可.
![]() 證明:連結
證明:連結![]() ,如圖,
,如圖,

∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切線;
的切線;
![]() 解:∵
解:∵![]() 的面積
的面積![]() 的面積
的面積![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
而![]() ,
,
∴![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某超市的某種商品一周內每天的進價與售價信息和實際每天的銷售量情況如圖表所示:
進價與售價折線圖(單位:元/斤)

實際銷售量表(單位:斤)
日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
銷售量 | 30 | 40 | 35 | 30 | 50 | 60 | 50 |
則下列推斷不合理的是( )
A. 該商品周一的利潤最小
B. 該商品周日的利潤最大
C. 由一周中的該商品每天售價組成的這組數據的眾數是4(元/斤)
D. 由一周中的該商品每天進價組成的這組數據的中位數是3(元/斤)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知直線y=-2x+4與x軸、y軸分別交于點A、C,以OA、OC為邊在第一象限內作長方形OABC.

(1)求點A、C的坐標;
(2)將△ABC對折,使得點A的與點C重合,折痕交AB于點D,求直線CD的解析式(圖②);
(3)在坐標平面內,是否存在點P(除點B外),使得△APC與△ABC全等?若存在,請直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
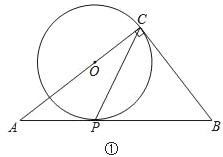
【題目】在△ABC中,∠ACB=90°,經過點C的⊙O與斜邊AB相切于點P.
(1)如圖①,當點O在AC上時,試說明2∠ACP=∠B;
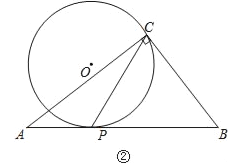
(2)如圖②,AC=8,BC=6,當點O在△ABC外部時,求CP長的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
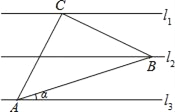
【題目】如圖,已知l1∥l2∥l3,相鄰兩條平行直線間的距離相等,若等腰直角三角形ABC的直角頂點C在l1上,另兩個頂點A,B分別在l3,l2上,則sinα的值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于點A(﹣3,m+8),B(n,﹣6)兩點.
的圖象交于點A(﹣3,m+8),B(n,﹣6)兩點.
(1)求一次函數與反比例函數的解析式;
(2)求△AOB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,點![]() 為坐標原點,
為坐標原點,![]() 的頂點
的頂點![]() 的坐標為
的坐標為![]() ,頂點
,頂點![]() 在
在![]() 軸上(點
軸上(點![]() 在點
在點![]() 的右側),點
的右側),點![]() 在
在![]() 上,連接
上,連接![]() ,且
,且![]() .
.
(1)如圖1,求點![]() 的縱坐標;
的縱坐標;
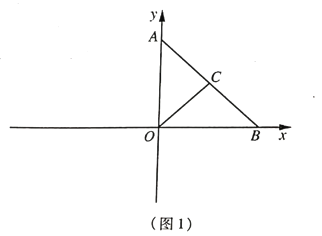
(2)如圖2,點![]() 在
在![]() 軸上(點
軸上(點![]() 在點
在點![]() 的左側),點
的左側),點![]() 在
在![]() 上,連接
上,連接![]() 交
交![]() 于點
于點![]() ;若
;若![]() ,求證:
,求證:![]()
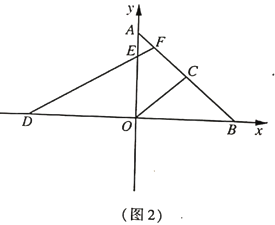
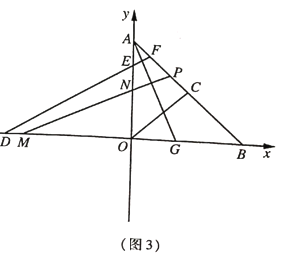
(3)如圖3,在(2)的條件下,![]() 是
是![]() 的角平分線,點
的角平分線,點![]() 與點
與點![]() 關于
關于![]() 軸對稱,過點
軸對稱,過點![]() 作
作![]() 分別交
分別交![]() 于點
于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com