
【題目】如圖,拋物線L:y=﹣ ![]() (x﹣t)(x﹣t+4)(常數t>0)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y=
(x﹣t)(x﹣t+4)(常數t>0)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y= ![]() (k>0,x>0)于點P,且OAMP=12.
(k>0,x>0)于點P,且OAMP=12.
(1)求k的值;
(2)當t=1時,求AB長,并求直線MP與L對稱軸之間的距離;
(3)把L在直線MP左側部分的圖象(含與直線MP的交點)記為G,用t表示圖象G最高點的坐標.
【答案】
(1)
解:設P(x,y)則MP=y,
∵M為OA的中點,
∴OA=2x,
∵OAMP=12,
∴2xy=12,
∴xy=6,
∴k=6
(2)
解:當t=1,y=0時,0=﹣ ![]() (x﹣1)(x﹣1+4),解得x=1或x=﹣3,
(x﹣1)(x﹣1+4),解得x=1或x=﹣3,
∴A(1,0)、B(﹣3,0),
∴AB=4;
∴拋物線L的對稱軸為直線x= ![]() =﹣1,
=﹣1,
∵OA=1,
∴MP為直線x= ![]() ,
,
∴直線MP與L對稱軸之間的距離為 ![]()
(3)
解:在y=﹣ ![]() (x﹣t)(x﹣t+4)中,令y=0可得﹣
(x﹣t)(x﹣t+4)中,令y=0可得﹣ ![]() (x﹣t)(x﹣t+4)=0,解得x=t或x=t﹣4,
(x﹣t)(x﹣t+4)=0,解得x=t或x=t﹣4,
∴A(t,0),B(t﹣4,0),
∴拋物線L的對稱軸為直線x= ![]() =t﹣2,
=t﹣2,
又∵MP為直線x= ![]() ,
,
∴當拋物線L的頂點在直線MP上或左側時,即t﹣2≤ ![]() 時,解得t≤4,此時,頂點(t﹣2,2)為圖象G最高點的坐標;
時,解得t≤4,此時,頂點(t﹣2,2)為圖象G最高點的坐標;
當拋物線L的頂點在直線MP右側時,即t﹣2> ![]() 時,解得t>4,此時時,交點直線MP與拋物線L的交點為(
時,解得t>4,此時時,交點直線MP與拋物線L的交點為( ![]() ,﹣
,﹣ ![]() t2+t),為圖象G最高點的坐標
t2+t),為圖象G最高點的坐標
【解析】(1)設P(x,y),則可表示出MP,由M為OA的中點,可求得OA,由條件可求得xy,則可求得k的值;(2)把t=1,代入拋物線解析式,令y=0可求得A、B兩點的坐標,可求得AB的長,再求得拋物線的對稱軸和直線MP的方程,可求得直線MP與對稱軸之間的距離;(3)可用t表示出A、B兩點的坐標,進一步可表示出直線MP的解析式,再根據頂點的位置可求得其最大值,可表示出G的坐標.
【考點精析】解答此題的關鍵在于理解反比例函數的概念的相關知識,掌握形如y=k/x(k為常數,k≠0)的函數稱為反比例函數.自變量x的取值范圍是x不等于0的一切實數,函數的取值范圍也是一切非零實數,以及對反比例函數的圖象的理解,了解反比例函數的圖像屬于雙曲線.反比例函數的圖象既是軸對稱圖形又是中心對稱圖形.有兩條對稱軸:直線y=x和 y=-x.對稱中心是:原點.


科目:初中數學 來源: 題型:
【題目】現今“微信運動”被越來越多的人關注和喜愛,某興趣小組隨機調查了我市50名教師某日“微信運動”中的步數情況進行統計整理,繪制了如下的統計圖表(不完整):
步數 | 頻數 | 頻率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
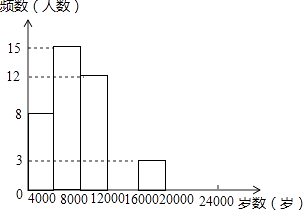
請根據以上信息,解答下列問題:
(1)寫出a,b,c,d的值并補全頻數分布直方圖;
(2)本市約有37800名教師,用調查的樣本數據估計日行走步數超過12000步(包含12000步)的教師有多少名?
(3)若在50名被調查的教師中,選取日行走步數超過16000步(包含16000步的兩名教師與大家分享心得,求被選取的兩名教師恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E、F、G、H分別為四邊形ABCD的四邊AB、BC、CD、DA的中點,則關于四邊形EFGH,下列說法正確的為( ) 
A.一定不是平行四邊形
B.一定不是中心對稱圖形
C.可能是軸對稱圖形
D.當AC=BD時它是矩形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知λ∈R,函數f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的導數為g(x).
(1)求曲線y=f(x)在x=1處的切線方程;
(2)若函數g(x)存在極值,求λ的取值范圍;
(3)若x≥1時,f(x)≥0恒成立,求λ的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把拋物線y= ![]() x2平移得到拋物線m,拋物線m經過點A(﹣6,0)和原點O(0,0),它的頂點為P,它的對稱軸與拋物線y=
x2平移得到拋物線m,拋物線m經過點A(﹣6,0)和原點O(0,0),它的頂點為P,它的對稱軸與拋物線y= ![]() x2交于點Q,則圖中陰影部分的面積為 .
x2交于點Q,則圖中陰影部分的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為豐富居民業余生活,某居民區組建籌委會,該籌委會動員居民自愿集資建立一個書刊閱覽室.經預算,一共需要籌資30000元,其中一部分用于購買書桌、書架等設施,另一部分用于購買書刊.
(1)籌委會計劃,購買書刊的資金不少于購買書桌、書架等設施資金的3倍,問最多用多少資金購買書桌、書架等設施?
(2)經初步統計,有200戶居民自愿參與集資,那么平均每戶需集資150元.鎮政府了解情況后,贈送了一批閱覽室設施和書籍,這樣,只需參與戶共集資20000元.經籌委會進一步宣傳,自愿參與的戶數在200戶的基礎上增加了a%(其中a>0).則每戶平均集資的資金在150元的基礎上減少了 ![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y= ![]() ,當x>0時,y隨x的增大而增大,則關于x的方程ax2﹣2x+b=0的根的情況是( )
,當x>0時,y隨x的增大而增大,則關于x的方程ax2﹣2x+b=0的根的情況是( )
A.有兩個正根
B.有兩個負根
C.有一個正根一個負根
D.沒有實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知拋物線C1、C2關于x軸對稱,拋物線C1 , C3關于y軸對稱,如果拋物線C2的解析式是y=﹣ ![]() (x﹣2)2+2,那么拋物線C3的解析式是( )
(x﹣2)2+2,那么拋物線C3的解析式是( ) 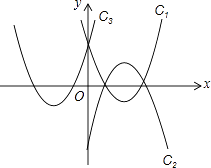
A.y=﹣ ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
B.y=﹣ ![]() (x+2)2+2??
(x+2)2+2??
C.y= ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
D.y= ![]() (x+2)2﹣2
(x+2)2﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知AB為⊙O的直徑,CD是弦,且AB⊥CD于點E.連接AC、OC、BC. 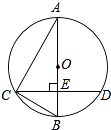
(1)求證:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的直徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com