
【題目】勾股定理是一條古老的數學定理,它有很多種證明方法,我國漢代數學家趙爽根據弦圖,利用面積法進行證明,著名數學家華羅庚曾提出把“數形關系”(勾股定理)帶到其他星球,作為地球人與其他星球“人”進行第一次“談話”的語言.
[定理表述]
請你寫出勾股定理內容(用文字語言表述):
[嘗試證明]
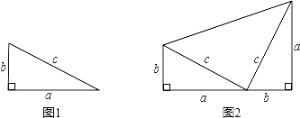
以圖1中的直角三角形為基礎,可以構造出以a、b為底,以(a+b)為高的直角梯形(如圖2),請你利用圖2,證明勾股定理.
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】P點在平面直角坐標系的第二象限,P到x軸的距離為1,到y軸的距離為2,則P點的坐標是( )
A. (-1,2) B. (-2,1) C. (1,-2) D. (2,-1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名同學投擲實心球,每人投10次,平均成績為18米,方差分別為S甲2=0.1,S乙2=0.04,成績比較穩定的是__(填“甲”或“乙”).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店把一本新書按標價的九折出售,仍可獲利20%.若該書的進價為21元,則標價為( )
A. 26元 B. 27元 C. 28元 D. 29元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,F是BC上一點,FG⊥AB,垂足為G.
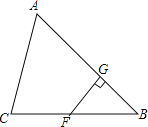
(1)過C點畫CD⊥AB,垂足為D;
(2)過D點畫DE∥BC,交AC于E;
(3)求證:∠EDC=∠GFB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在Rt△ABC中,∠ACB=90°,AC=BC,BM⊥CM于M,且CM>BM
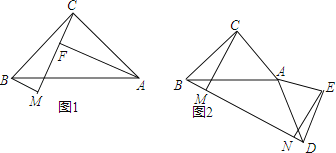
(1)如圖1,過點A作AF⊥CM于F,直線寫出線段BM、AF、MF的數量關系是
(2)如圖2,D為BM延長線上一點,連AD以AD為斜邊向右側作等腰Rt△ADE,再過點E作EN⊥BM于N,求證:CM+EN=MN;
(3)將(2)中的△ADE繞點A順時針旋轉任意角α后,連BD取BD中點P,連CP、EP,作出圖形,試判斷CP、EP的數量和位置關系并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com