
【題目】已知,點O在線段AB上,AB=6,OC為射線,且∠BOC=45°.動P以每秒1個單位長度的速度從點O出發,沿射線OC做勻速運動.設運動時間為t 秒.

(1)如圖1,若AO=2.
①當 t=6秒時,則OP= ,S△ABP= ;
②當△ABP與△PBO相似時,求t的值;
(2)如圖2,若點O為線段AB的中點,當AP=AB時,過點A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.
【答案】(1)①6;![]() ;②t=
;②t=![]() +4;(2)18.
+4;(2)18.
【解析】
試題分析:(1)①如圖1中,作PE⊥AB于E.求出PE的長,根據S△APB=![]() ABPE,即可計算.
ABPE,即可計算.
②如圖1中,過點B作OC的垂線,垂足為H,由△ABP∽△PBO,得![]() ,即PB2=BOBA=24,推出BP=
,即PB2=BOBA=24,推出BP=![]() ,再利用勾股定理求出OH、HP即可解決問題.
,再利用勾股定理求出OH、HP即可解決問題.
(2)如圖中,作OE∥AP,交BP于點E.由△QAO∽△OEP,得![]() ,即AQEP=EOAO,由三角形中位線定理得OE=3,推出AQEP=9,由此即可解決問題.
,即AQEP=EOAO,由三角形中位線定理得OE=3,推出AQEP=9,由此即可解決問題.
試題解析:(1)①如圖1中,作PE⊥AB于E.
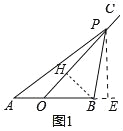
在Rt△OPE中,OP=6,∠POE=45°,
∴PE=OPsin45°=3![]() ,
,
∴S△APB=![]() ABPE=9
ABPE=9![]() ,
,
②如圖1中,過點B作OC的垂線,垂足為H,
∵△ABP∽△PBO,
∴![]() ,
,
∴PB2=BOBA=24,
∴BP=![]() ,
,
在Rt△OHB中,∵∠BOH=45°,OB=4,
∴OH=HB=![]() ,
,
在Rt△PHB中,PH=![]() =4
=4
∴OP=![]() +4,
+4,
∴t=![]() +4(秒)時,△ABP∽△PBO.
+4(秒)時,△ABP∽△PBO.
(2)如圖中,作OE∥AP,交BP于點E.
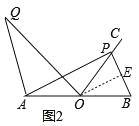
∵AP=AB,
∴∠APB=∠B,
∴∠OEB=∠APB=∠B,
∵AQ∥BP,
∴∠QAB+∠B=180°.
又∵∠OEP+∠OEB=180°,
∴∠OEP=∠QAB,
又∵∠AOC=∠2+∠B=∠1+∠QOP,
∵∠B=∠QOP,
∴∠AOQ=∠OPE,
∴△QAO∽△OEP,
∴![]() ,即AQEP=EOAO,
,即AQEP=EOAO,
由三角形中位線定理得OE=3,
∴AQEP=9,
AQBP=AQ2EP=2AQEP=18.


科目:初中數學 來源: 題型:
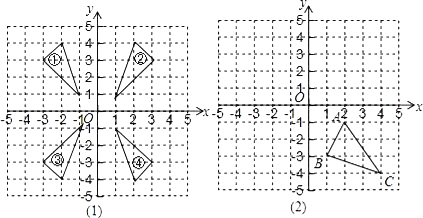
【題目】在圖(1)中編號①②③④的四個三角形中,關于y軸對稱的兩個三角形的編號為______;關于x軸對稱的兩個三角形的編號為______.在圖(2)中,畫出△ABC關于x軸對稱的圖形△A1B1C1,并分別寫出點A1,B1,C1的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,將坐標是(3,0),(3,2),(0,3),(3,5),(3,2),(6,3),(6,2),(3,0),(6,0)的點用線段依次連接起來形成一個圖案.
(1)作出原圖案關于x軸對稱的圖案.兩圖案中的對應點的坐標有怎樣的關系?
(2)作出原圖案關于y軸對稱的圖案.兩圖案中的對應點的坐標有怎樣的關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明有5張寫著以下數字的卡片,請你按要求抽出卡片,完成下列各題. ![]()
(1)從中取出2張卡片,使這2張卡片上數字乘積最大,最大值是 .
(2)從中取出2張卡片,使這2張卡片數字相除商最小,最小值是 .
(3)從中取出除0以外的4張卡片,將這4個數字進行加、減、乘、除或乘方等混合運算,使結果為24,(注:每個數字只能用一次,如:23×[1﹣(﹣2)]=8×3=24),請另寫出一種符合要求的運算式子 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com