
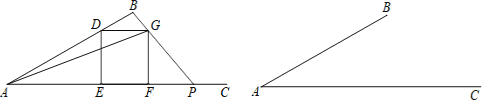
【題目】如圖1,![]() 的余切值為2,
的余切值為2,![]() ,點D是線段
,點D是線段![]() 上的一動點(點D不與點A、B重合),以點D為頂點的正方形
上的一動點(點D不與點A、B重合),以點D為頂點的正方形![]() 的另兩個頂點E、F都在射線
的另兩個頂點E、F都在射線![]() 上,且點F在點E的右側,聯結
上,且點F在點E的右側,聯結![]() ,并延長
,并延長![]() ,交射線
,交射線![]() 于點P.
于點P.
(1)點D在運動時,下列的線段和角中,________是始終保持不變的量(填序號);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() ;
;
(2)設正方形的邊長為x,線段![]() 的長為y,求y與x之間的函數關系式,并寫出定義域;
的長為y,求y與x之間的函數關系式,并寫出定義域;
(3)如果![]() 與
與![]() 相似,但面積不相等,求此時正方形的邊長.
相似,但面積不相等,求此時正方形的邊長.
【答案】(1)④⑤;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)作![]() 于M,交
于M,交![]() 于N,如圖,利用三角函數的定義得到
于N,如圖,利用三角函數的定義得到![]() ,設
,設![]() ,則
,則![]() ,利用勾股定理得
,利用勾股定理得![]() ,解得
,解得![]() ,即
,即![]() ,
,![]() ,設正方形的邊長為x,則
,設正方形的邊長為x,則![]() ,
,![]() ,由于
,由于![]() ,則可判斷
,則可判斷![]() 為定值;再利用
為定值;再利用![]() 得到
得到![]() ,則可判斷
,則可判斷![]() 為定值;在
為定值;在![]() 中,利用勾股定理和三角函數可判斷
中,利用勾股定理和三角函數可判斷![]() 在變化,
在變化,![]() 在變化,
在變化,![]() 在變化;
在變化;
(2)易得四邊形![]() 為矩形,則
為矩形,則![]() ,證明
,證明![]() ,利用相似比可得到y與x的關系式;
,利用相似比可得到y與x的關系式;
(3)由于![]() ,
,![]() 與
與![]() 相似,且面積不相等,利用相似比得到
相似,且面積不相等,利用相似比得到![]() ,討論:當點P在點F點右側時,則
,討論:當點P在點F點右側時,則![]() ,所以
,所以![]() ,當點P在點F點左側時,則
,當點P在點F點左側時,則![]() ,所以
,所以![]() ,然后分別解方程即可得到正方形的邊長.
,然后分別解方程即可得到正方形的邊長.
(1)如圖,作![]() 于M,交
于M,交![]() 于N,
于N,
在![]() 中,∵
中,∵![]() ,
,
設![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
設正方形的邊長為x,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() 為定值;
為定值;
∵![]() ,
,
∴![]() ,
,
∴![]() 為定值;
為定值;
在![]() 中,
中,![]() ,
,
而![]() 在變化,
在變化,
∴![]() 在變化,
在變化,![]() 在變化,
在變化,
∴![]() 在變化,
在變化,
所以![]() 和
和![]() 是始終保持不變的量;
是始終保持不變的量;

故答案為:④⑤
(2)∵MN⊥AP,DEFG是正方形,
∴四邊形![]() 為矩形,
為矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]()
(3)∵![]() ,
,![]() 與
與![]() 相似,且面積不相等,
相似,且面積不相等,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
當點P在點F點右側時,AP=AF+PF=![]() =
=![]() ,
,
∴![]() ,
,
解得![]() ,
,
當點P在點F點左側時,![]() ,
,
∴![]() ,
,
解得![]() ,
,

綜上所述,正方形的邊長為![]() 或
或![]() .
.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】 如圖,在直角坐標系中,矩形OABC的頂點O在坐標原點,邊OA在x軸上,
OC在y軸上,如果矩形OA′B′C′與矩形OABC關于點O位似,且矩形OA′B′C′的面積等于矩形OABC面積的![]() ,那么點B′的坐標是【 】
,那么點B′的坐標是【 】
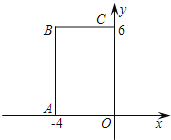
A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富校園文化生活,提高學生的綜合素質,促進中學生全面發展,學校開展了多種社團活動.小明喜歡的社團有:合唱社團、足球社團、書法社團、科技社團(分別用字母A,B,C,D依次表示這四個社團),并把這四個字母分別寫在四張完全相同的不透明的卡片的正面上,然后將這四張卡片背面朝上洗勻后放在桌面上.
(1)小明從中隨機抽取一張卡片是足球社團B的概率是 .
(2)小明先從中隨機抽取一張卡片,記錄下卡片上的字母后不放回,再從剩余的卡片中隨機抽取一張卡片,記錄下卡片上的字母.請你用列表法或畫樹狀圖法求出小明兩次抽取的卡片中有一張是科技社團D的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】婁底市某樓盤準備以每平方米5000元的均價對外銷售,由于國務院有關房地產的新政策出臺后,購房者持幣觀望.為了加快資金周轉,房地產開發商對價格經過兩次下調后,決定以每平方米4050元的均價開盤銷售.
(1)求平均每次下調的百分率;
(2)某人準備以開盤均價購買一套150平方米的房子.開發商還給予以下兩種優惠方案以供選擇:①打9.8折銷售;②不打折,送三年物業管理費.物業管理費為每平方米每月1.5元.請問哪種方案更優惠?
查看答案和解析>>
科目:初中數學 來源: 題型:
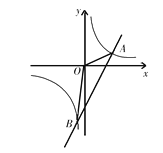
【題目】如圖,直線y1=3x﹣5與反比例函數y2=![]() 的圖象相交A(2,m),B(n,﹣6)兩點,連接OA,OB.
的圖象相交A(2,m),B(n,﹣6)兩點,連接OA,OB.
(1)求k和n的值;
(2)求△AOB的面積;
(3)直接寫出y1> y2時自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
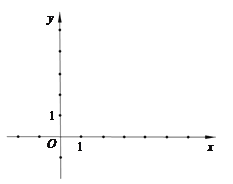
【題目】如圖,在平面直角坐標系![]() 中,直線y=kx+3與
中,直線y=kx+3與![]() 軸、
軸、![]() 軸分別相交于點A、B,并與拋物線
軸分別相交于點A、B,并與拋物線![]() 的對稱軸交于點
的對稱軸交于點![]() ,拋物線的頂點是點
,拋物線的頂點是點![]() .
.
(1)求k和b的值;
(2)點G是![]() 軸上一點,且以點
軸上一點,且以點![]() 、C、
、C、![]() 為頂點的三角形與△
為頂點的三角形與△![]() 相似,求點G的坐標;
相似,求點G的坐標;
(3)在拋物線上是否存在點E:它關于直線AB的對稱點F恰好在y軸上.如果存在,直接寫出點E的坐標,如果不存在,試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
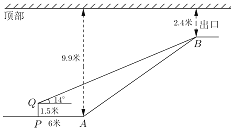
【題目】地鐵10號線某站點出口橫截面平面圖如圖所示,電梯![]() 的兩端分別距頂部9.9米和2.4米,在距電梯起點
的兩端分別距頂部9.9米和2.4米,在距電梯起點![]() 端6米的
端6米的![]() 處,用1.5米的測角儀測得電梯終端
處,用1.5米的測角儀測得電梯終端![]() 處的仰角為14°,求電梯
處的仰角為14°,求電梯![]() 的坡度與長度.(參考數據:
的坡度與長度.(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() ,
,![]()
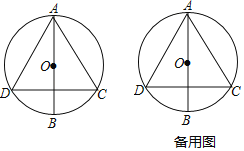
(1)求證:![]() 是等邊三角形.
是等邊三角形.
(2)若點![]() 是
是![]() 的中點,連接
的中點,連接![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,若
,若![]() ,求線段
,求線段![]() 的長;
的長;
(3)若![]() 的半徑為4,點
的半徑為4,點![]() 是弦
是弦![]() 的中點,點
的中點,點![]() 是直線
是直線![]() 上的任意一點,將點
上的任意一點,將點![]() 繞點
繞點![]() 逆時針旋轉60°得點
逆時針旋轉60°得點![]() ,求線段
,求線段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2﹣x+c的對稱軸為直線x=1,與x軸的一個交點為A(﹣1,0),頂點為B.點C(5,m)在拋物線上,直線BC交x軸于點E.
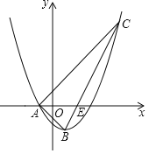
(1)求拋物線的表達式及點E的坐標;
(2)聯結AB,求∠B的正切值;
(3)點G為線段AC上一點,過點G作CB的垂線交x軸于點M(位于點E右側),當△CGM與△ABE相似時,求點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com