
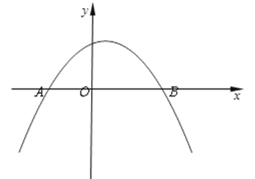
【題目】如圖,已知平面直角坐標(biāo)系![]() ,拋物線
,拋物線![]() 與
與![]() 軸交于點(diǎn)A(-2,0)和點(diǎn)B(4,0) .
軸交于點(diǎn)A(-2,0)和點(diǎn)B(4,0) .
(1)求這條拋物線的表達(dá)式和對稱軸;
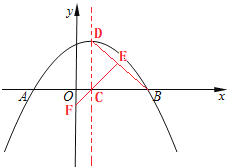
(2)點(diǎn)C在線段OB上,過點(diǎn)C作CD⊥![]() 軸,垂足為點(diǎn)C,交拋物線與點(diǎn)D,E是BD中點(diǎn),聯(lián)結(jié)CE并延長,與
軸,垂足為點(diǎn)C,交拋物線與點(diǎn)D,E是BD中點(diǎn),聯(lián)結(jié)CE并延長,與![]() 軸交于點(diǎn)F.
軸交于點(diǎn)F.
①當(dāng)D恰好是拋物線的頂點(diǎn)時(shí),求點(diǎn)F的坐標(biāo);
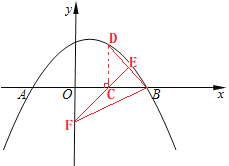
②聯(lián)結(jié)BF,當(dāng)△DBC的面積是△BCF面積的![]() 時(shí),求點(diǎn)C的坐標(biāo).
時(shí),求點(diǎn)C的坐標(biāo).
【答案】(1) ![]() ,x=1;(2)①F的坐標(biāo)是(0,
,x=1;(2)①F的坐標(biāo)是(0,![]() );②C坐標(biāo)是
);②C坐標(biāo)是![]() .
.
【解析】
(1)用待定系數(shù)法求解;
(2)①求出頂點(diǎn)坐標(biāo),得出DC、OC、BC長度,在Rt△DCB和Rt△OFC中,利用三角函數(shù)求出OF值即可;
②通過面積比找到DC與OF比值,證明△DCB∽△FOC,借助比例式求解OB,從而得到OC長.
(1)由題意得,拋物線![]() 經(jīng)過點(diǎn)A(-2,0)和點(diǎn)B(4,0),
經(jīng)過點(diǎn)A(-2,0)和點(diǎn)B(4,0),
代入得![]() 解得
解得 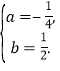
因此,這條拋物線的表達(dá)式是![]() .
.
它的對稱軸是直線![]() .
.
(2)①由拋物線的表達(dá)式![]() ,得頂點(diǎn)D的坐標(biāo)是(1,
,得頂點(diǎn)D的坐標(biāo)是(1,![]() ).
).
∴![]() .
.
∵D是拋物線頂點(diǎn),CD⊥![]() 軸,E是BD中點(diǎn),∴
軸,E是BD中點(diǎn),∴![]() . ∴
. ∴![]() .
.
∵![]() ,∴
,∴![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,![]() .∴點(diǎn)F的坐標(biāo)是(0,
.∴點(diǎn)F的坐標(biāo)是(0,![]() ).
).
②∵![]() ,
,![]() , ∴
, ∴![]() .
.
∵△DBC的面積是△BCF面積的![]() , ∴
, ∴![]() .
.
由①得![]() ,又
,又![]() ,
,
∴△![]() ∽△
∽△![]() .∴
.∴![]() .
.
又OB=4,∴![]() ,∴
,∴![]() .即點(diǎn)C坐標(biāo)是
.即點(diǎn)C坐標(biāo)是![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線![]() :
:![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于
軸交于![]() 點(diǎn),拋物線
點(diǎn),拋物線![]() 經(jīng)過
經(jīng)過![]() ,
,![]() 兩點(diǎn),且與
兩點(diǎn),且與![]() 軸交于另一點(diǎn)
軸交于另一點(diǎn)![]() .
.
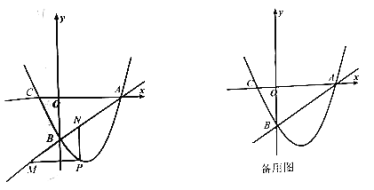
(1)求直線及拋物線的解析式;
(2)點(diǎn)![]() 是拋物線上一動(dòng)點(diǎn),當(dāng)點(diǎn)
是拋物線上一動(dòng)點(diǎn),當(dāng)點(diǎn)![]() 在直線
在直線![]() 下方的拋物線上運(yùn)動(dòng)時(shí),過點(diǎn)
下方的拋物線上運(yùn)動(dòng)時(shí),過點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,求
,求![]() 的最大值;
的最大值;
(3)在(2)的條件下,當(dāng)![]() 的值最大時(shí),將
的值最大時(shí),將![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn),當(dāng)點(diǎn)
旋轉(zhuǎn),當(dāng)點(diǎn)![]() 落在
落在![]() 軸上時(shí),直接寫出此時(shí)點(diǎn)
軸上時(shí),直接寫出此時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
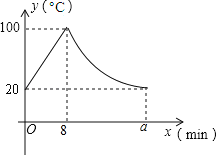
【題目】某小學(xué)為每個(gè)班級配備了一種可以加熱的飲水機(jī),該飲水機(jī)的工作程序是:放滿水后,接通電源,則自動(dòng)開始加熱,每分鐘水溫上升10℃,待加熱到100℃,飲水機(jī)自動(dòng)停止加熱,水溫開始下降,水溫y(℃)與通電時(shí)間x(min)成反比例關(guān)系,直至水溫降至室溫,飲水機(jī)再次自動(dòng)加熱,重復(fù)上述過程.設(shè)某天水溫和室溫為20℃,接通電源后,水溫y(℃)與通電時(shí)間x(min)的關(guān)系如下圖所示,回答下列問題:
(1)當(dāng)0≤x≤8時(shí),求y與x之間的函數(shù)關(guān)系式;
(2)求出圖中a的值;
(3)某天早上7:20,李老師將放滿水后的飲水機(jī)電源打開,若他想在8:00上課前能喝到不超過40℃的溫開水,問:他應(yīng)在什么時(shí)間段內(nèi)接水?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)為推動(dòng)“時(shí)刻聽黨話 永遠(yuǎn)跟黨走”校園主題教育活動(dòng),計(jì)劃開展四項(xiàng)活動(dòng):A:黨史演講比賽,B:黨史手抄報(bào)比賽,C:黨史知識競賽,D:紅色歌詠比賽.校團(tuán)委對學(xué)生最喜歡的一項(xiàng)活動(dòng)進(jìn)行調(diào)查,隨機(jī)抽取了部分學(xué)生,并將調(diào)查結(jié)果繪制成圖1,圖2兩幅不完整的統(tǒng)計(jì)圖.請結(jié)合圖中信息解答下列問題:
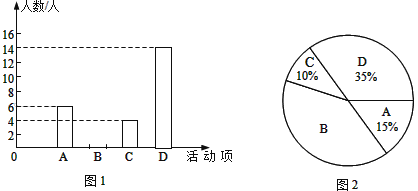
(1)本次共調(diào)查了 名學(xué)生;
(2)將圖1的統(tǒng)計(jì)圖補(bǔ)充完整;
(3)已知在被調(diào)查的最喜歡“黨史知識競賽”項(xiàng)目的4個(gè)學(xué)生中只有1名女生,現(xiàn)從這4名學(xué)生中任意抽取2名學(xué)生參加該項(xiàng)目比賽,請用畫樹狀圖或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在證明“勾股定理”時(shí),可以將4個(gè)全等的直角三角形和一個(gè)小正方形拼成的一個(gè)大正方形(如圖所示).如果小正方形的面積是25,大正方形的面積為49,直角三角形中較小的銳角為α,那么tanα的值是____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一批貨物準(zhǔn)備運(yùn)往某地,有甲、乙、丙三輛卡車可雇用.已知甲、乙、丙三輛車每次運(yùn)貨量不變,且甲、乙兩車單獨(dú)運(yùn)完這批貨物分別用![]() 次;甲、丙兩車合運(yùn)相同次數(shù),運(yùn)完這批貨物,甲車共運(yùn)
次;甲、丙兩車合運(yùn)相同次數(shù),運(yùn)完這批貨物,甲車共運(yùn)![]() 噸;乙、丙兩車合運(yùn)相同次數(shù),運(yùn)完這批貨物乙車共運(yùn)
噸;乙、丙兩車合運(yùn)相同次數(shù),運(yùn)完這批貨物乙車共運(yùn)![]() 噸,現(xiàn)甲、乙、丙合運(yùn)相同次數(shù)把這批貨物運(yùn)完,貨主應(yīng)付甲車主的運(yùn)費(fèi)為___________ 元.(按每噸運(yùn)費(fèi)
噸,現(xiàn)甲、乙、丙合運(yùn)相同次數(shù)把這批貨物運(yùn)完,貨主應(yīng)付甲車主的運(yùn)費(fèi)為___________ 元.(按每噸運(yùn)費(fèi)![]() 元計(jì)算)
元計(jì)算)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
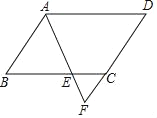
【題目】如圖,在![]() 中,點(diǎn)
中,點(diǎn)![]() 在
在![]() 邊上,
邊上,![]() 的延長線交于點(diǎn)
的延長線交于點(diǎn)![]() ,下列結(jié)論錯(cuò)誤的是( )
,下列結(jié)論錯(cuò)誤的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解全區(qū)5000名初中畢業(yè)生的體重情況,隨機(jī)抽測了200名學(xué)生的體重,頻率分布如圖所示(每小組數(shù)據(jù)可含最小值,不含最大值),其中從左至右前四個(gè)小長方形的高依次為0.02、0.03、0.04、0.05,由此可估計(jì)全區(qū)初中畢業(yè)生的體重不小于60千克的學(xué)生人數(shù)約為___人.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線![]() 與拋物線
與拋物線![]() 相交于點(diǎn)
相交于點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 兩點(diǎn).
兩點(diǎn).
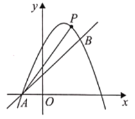
(1)求拋物線的函數(shù)表達(dá)式;
(2)若點(diǎn)![]() 是位于直線
是位于直線![]() 上方拋物線上的一動(dòng)點(diǎn),當(dāng)
上方拋物線上的一動(dòng)點(diǎn),當(dāng)![]() 的面積
的面積![]() 最大時(shí),求此時(shí)
最大時(shí),求此時(shí)![]() 的面積
的面積![]() 及點(diǎn)
及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使
,使![]() 是等腰三角形?若存在,直接寫出
是等腰三角形?若存在,直接寫出![]() 點(diǎn)的坐標(biāo)(不用說理);若不存在,請說明理由.
點(diǎn)的坐標(biāo)(不用說理);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com