
科目:初中數學 來源: 題型:
小明在課外學習時遇到這樣一個問題:
定義:如果二次函數y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常數)與y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常數)滿足a1+a2=0,b1=b2,c1+c2=0,則稱這兩個函數互為“旋轉函數”.
求函數y=﹣x2+3x﹣2的“旋轉函數”.
小明是這樣思考的:由函數y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根據a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能確定這個函數的“旋轉函數”.
請參考小明的方法解決下面問題:
(1)寫出函數y=﹣x2+3x﹣2的“旋轉函數”;
(2)若函數y=﹣x2+ mx﹣2與y=x2﹣2nx+n互為“旋轉函數”,求(m+n)2015的值;
mx﹣2與y=x2﹣2nx+n互為“旋轉函數”,求(m+n)2015的值;
(3)已知函數y=﹣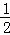 (x+1)(x﹣4)的圖象與x軸交于點A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分布是A1,B1,C1,試證明經過點A1,B1,C1的二次函數與函數y=﹣
(x+1)(x﹣4)的圖象與x軸交于點A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分布是A1,B1,C1,試證明經過點A1,B1,C1的二次函數與函數y=﹣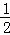 (x+1)(x﹣4)互為“旋轉函數.”
(x+1)(x﹣4)互為“旋轉函數.”
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,△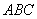 中,AB=AC
中,AB=AC ,D是BC的中點,AC的垂直平分線分
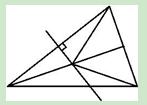
,D是BC的中點,AC的垂直平分線分 別交 AC、AD、AB于點E、O、F,則圖中全等的三角形的對數是
別交 AC、AD、AB于點E、O、F,則圖中全等的三角形的對數是
A.1對 B.2對 C.3對 D.4對
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數
已知二次函數 的圖像經過點
的圖像經過點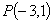 ,對稱軸是經過
,對稱軸是經過 且平行于
且平行于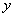 軸的直線。(1)求
軸的直線。(1)求 、
、 的值;
的值;
(2)如圖,一次函數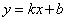 的圖像經過點
的圖像經過點 ,與
,與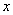 軸相交于點
軸相交于點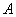 ,與二次函數的圖像相交于另一點B,點B在點P的右側,
,與二次函數的圖像相交于另一點B,點B在點P的右側, , 求一次函數的表達式。
, 求一次函數的表達式。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com