
���}Ŀ����D1������![]() �[����ƽ��ֱ������(bi��o)ϵ�У��c(di��n)
�[����ƽ��ֱ������(bi��o)ϵ�У��c(di��n)![]() ��
��![]() �S�ϣ��c(di��n)
�S�ϣ��c(di��n)![]() ��
��![]() �S�ϣ�
�S�ϣ�![]() ��
��![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��������
��ֱ��������![]() ��߅
��߅![]() ���c(di��n)
���c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ���c�c(di��n)
���c�c(di��n)![]() ��
��![]() �غϣ��^�c(di��n)
�غϣ��^�c(di��n)![]() ��
��![]() ��
��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ����
����![]() �S���c(di��n)
�S���c(di��n)![]() ��
��
��1����![]() �����ֱ�������Σ�
�����ֱ�������Σ�
����ֱ��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
����![]() �S������һ�c(di��n)
�S������һ�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��Ո(q��ng)?ji��n)�ֱ��
��Ո(q��ng)?ji��n)�ֱ��![]() ��
��![]() �S�Ϸքe��һ�c(di��n)
�S�Ϸքe��һ�c(di��n)![]() ��
��![]() ��ʹ
��ʹ![]() �����L��С��������˕r(sh��)�c(di��n)
�����L��С��������˕r(sh��)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���L����Сֵ��
���L����Сֵ��
��2����D2���^�c(di��n)![]() ��
��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����c(di��n)����߅����ƽ����߅�Σ���ֱ��
����c(di��n)����߅����ƽ����߅�Σ���ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
���𰸡���1����ֱ��![]() ����ʽ
����ʽ![]() �� ��N(0,
�� ��N(0,![]() ),
),![]() ���L����Сֵ��
���L����Сֵ��![]() ����2��
����2��![]() .
.
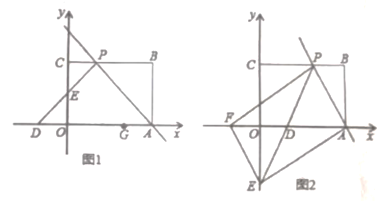
��������
��1�������þ��ε����|(zh��)�_��A��B��C�c(di��n)������(bi��o)�������õ������ǵ����|(zh��)�_��![]() ������
������![]() ���_��P�c(di��n)������(bi��o)���ٸ���(j��)A�c(di��n)������(bi��o)�_���_��ֱ��AP�ĺ���(sh��)���_(d��)ʽ. ����G�c(di��n)�P(gu��n)��y�S��(du��)�Q�c(di��n)G'(-2,0)�����c(di��n)G�P(gu��n)��ֱ��AP��(du��)�Q�c(di��n)G'(3,1)
���_��P�c(di��n)������(bi��o)���ٸ���(j��)A�c(di��n)������(bi��o)�_���_��ֱ��AP�ĺ���(sh��)���_(d��)ʽ. ����G�c(di��n)�P(gu��n)��y�S��(du��)�Q�c(di��n)G'(-2,0)�����c(di��n)G�P(gu��n)��ֱ��AP��(du��)�Q�c(di��n)G'(3,1)
�B��G'G'��y�S��N����ֱ��AP��M���˕r(sh��)��GMN���L����С����2���^P��PM��AD��M���ȸ���(j��)����������������һ�����|(zh��)�C��DM=MA ���ٸ���(j��)�ǽ�߅�����C����ODE�զ�MDP������(j��)ȫ�������ε����|(zh��)����c(di��n)P��D������(bi��o)������ֱ������ʽ��k=2,b=-2������ֱ��PE�Ľ���ʽ��y=2x-2.
��1���١߾���![]() ��
��![]()
��![]() ��
��
![]()
��![]() �����ֱ��������
�����ֱ��������
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�O(sh��)ֱ��![]() ����ʽ
����ʽ![]() ���^�c(di��n)
���^�c(di��n)![]() ���c(di��n)
���c(di��n)![]()
��![]() ��
��![]()
��ֱ��![]() ����ʽ
����ʽ![]()
����![]() �c(di��n)�P(gu��n)��
�c(di��n)�P(gu��n)��![]() �S��(du��)�Q�c(di��n)
�S��(du��)�Q�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �P(gu��n)��ֱ��
�P(gu��n)��ֱ��![]() ��(du��)�Q�c(di��n)
��(du��)�Q�c(di��n)![]()
�B��![]() ��
��![]() �S��
�S��![]() ����ֱ��
����ֱ��![]() ��
��![]() ���˕r(sh��)
���˕r(sh��)![]() ���L����С��
���L������

��![]()
��ֱ��![]() ����ʽ
����ʽ![]()
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����
����![]()
��![]()
��![]() ���L����Сֵ��
���L����Сֵ��![]()
��2����D����![]() ��
��![]()

��![]() ��
��![]() ��
��![]()
��![]() ����
����![]() ��
��![]()
����߅��![]() ��ƽ����߅�� ��
��ƽ����߅�� ��![]()
�֡�![]()
��![]()
��![]() ��
��![]()
��![]() ��
��![]()
��![]()
�O(sh��)ֱ��![]() �Ľ���ʽ
�Ľ���ʽ![]()
![]() ��
��![]()
��ֱ��![]() ����ʽ
����ʽ![]()


 ABC����ȫ��(y��u)��ϵ�д�
ABC����ȫ��(y��u)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��С���ڽ�Q���}����֪a=![]() ����2a2��8a+1��ֵ�������@�ӷ����c��ģ�
����2a2��8a+1��ֵ�������@�ӷ����c��ģ�
��a=![]() =
= =2��
=2��![]()
��a��2=��![]()
�ࣨa��2��2=3��a2��4a+4=3
��a2��4a=��1
��2a2��8a+1=2��a2��4a��+1=2������1��+1=��1
Ո(q��ng)�����(j��)С���ķ����^�̣���Q�����}��
��1������![]() +
+![]() +
+![]() +��+
+��+![]()
��2����a=![]() ����4a2��8a+1��ֵ��
����4a2��8a+1��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ώ��S�C(j��)����˱��W(xu��)�ڌW(xu��)���x�n�����(c��)��(sh��)����r���L�Ƴɲ������ėl�νy(t��ng)Ӌ(j��)�D�Ͳ����������νy(t��ng)Ӌ(j��)�D����D��ʾ����

��1���a(b��)ȫ�l�νy(t��ng)Ӌ(j��)�D��
��2��������νy(t��ng)Ӌ(j��)�D�Ѓ�(c��)��(sh��)��4�����εĈA�ĽǵĶȔ�(sh��)��
��3���ώ��S�����a(b��)����������ˣ���֪���ٵ��x��6��(c��)�������c֮ǰ�Ĕ�(sh��)��(j��)�ϲ���l(f��)�F(xi��n)��(c��)��(sh��)����λ��(sh��)�]��׃���t����a(b��)������ ����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ЌW(xu��)���w�|(zh��)�����C���u(p��ng)���ɿ�?y��u)?/span>x�֣��M�֞�100�֣�Ҏ(gu��)����85��x��100��A��(j��)��75��x��85��B��(j��)��60��x��75��C��(j��)��x��60��D��(j��)���F(xi��n)�S�C(j��)��ȡ�����ЌW(xu��)���W(xu��)���ľC���u(p��ng)���ɿ��������L�Ƴ����ɷ��������Ľy(t��ng)Ӌ(j��)�D��Ո(q��ng)����(j��)�D�е���Ϣ��������І��}��
��1�����@���{(di��o)���У�һ����ȡ���� �����W(xu��)������=�� ��%��
��2���a(b��)ȫ�l�νy(t��ng)Ӌ(j��)�D���������νy(t��ng)Ӌ(j��)�D��C��(j��)��(du��)��(y��ng)�ĈA�ĽǞ��� ���ȣ�
��3����ԓУ����2000���W(xu��)����Ո(q��ng)���Ӌ(j��)ԓУD��(j��)�W(xu��)���ж�������

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
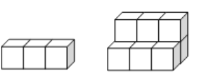
���}Ŀ����D�����������ǶՉ�ʯ�ݣ��D�քe��ʾ����һ�����A�ݕr(sh��)����r����ô���@�Ӊ���ȥ
һ��(j��) ����(j��)
������±���δ��ăɿգ��^��Ҏ(gu��)�ɡ�
�A�ݼ�(j��)��(sh��) | һ��(j��) | ����(j��) | ����(j��) | �ļ�(j��) |
ʯ�ՉK��(sh��) | 3 | 9 |
�ڵ���n��(j��)�A�ݕr(sh��)�����������wʯ��_______________�K����n�Ĵ���(sh��)ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ABC��һ�Kֱ�����ǿ��ҡ�C=90������A=30�����F(xi��n)���A�Ğ��c(di��n)O�ĈA�μ�Ƭ���������ǿ��(n��i)�������A�μ�Ƭ�������ǿ�ă�(n��i)��߅���L��(d��ng)1�ܣ��ص����c(di��n)λ�Õr(sh��)ֹͣ����BC=9���A�μ�Ƭ�İ돽��2���t�A��O�\(y��n)��(d��ng)��·���L��_____��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������˽�ijУ�W(xu��)�����n����x��r���S�C(j��)�����![]() ���W(xu��)������x�Õr(sh��)��(sh��)���Y(ji��)�����±���
���W(xu��)������x�Õr(sh��)��(sh��)���Y(ji��)�����±���
����x�Õr(sh��)��(sh��)(С�r(sh��)) | 4 | 5 | 8 | 12 |
�W(xu��)���˔�(sh��)(��) | 3 | 4 | 2 | 1 |
�t�P(gu��n)���@![]() ���W(xu��)������x���Õr(sh��)�g�������f�����_����( )
���W(xu��)������x���Õr(sh��)�g�������f�����_����( )
A. ���(sh��)��![]() B. ����(sh��)��
B. ����(sh��)��![]() C. ƽ����(sh��)��
C. ƽ����(sh��)��![]() D. ������
D. ������![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��Ӌ(j��)�㣺
��1����0.5+3![]() +2.6��5
+2.6��5![]() +1.15��
+1.15��
��2����81��|��2![]() |��
|��![]() �£���16����
�£���16����
��3������2��3+����1![]() ��2��
��2��![]() +��
+��![]() ��������18����
��������18����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(sh��)![]() ��b�ڔ�(sh��)�S�ϵ�λ����D��ʾ��
��b�ڔ�(sh��)�S�ϵ�λ����D��ʾ��
![]()
��1�� a+b 0 , a-b 0�� �����������=��������
��2�� ������|a|-|b|+|a-b|
��3���ڔ�(sh��)�S�ϱ�ʾa+b�ca-b������![]() ��b��0��a+b��a-b����С��������á������B��������
��b��0��a+b��a-b����С��������á������B��������
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com