
已知拋物線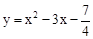 的頂點為點D,并與x軸相交于A、B兩點(點A在點B的左側),與y軸相交于點C.
的頂點為點D,并與x軸相交于A、B兩點(點A在點B的左側),與y軸相交于點C.
(1)求點A、B、C、D的坐標;
(2)在y軸的正半軸上是否存在點P,使以點P、O、A為頂點的三角形與△AOC相似?若存在,求出點P的坐標;若不存在,請說明理由;
(3)取點E(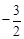 ,0)和點F(0,
,0)和點F(0,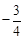 ),直線l經過E、F兩點,點G是線段BD的中點.
),直線l經過E、F兩點,點G是線段BD的中點.
①點G是否在直線l上,請說明理由;
②在拋物線上是否存在點M,使點M關于直線l的對稱點在x軸上?若存在,求出點M的坐標;若不存在,請說明理由.
解:(1)在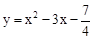 中,令y=0,則
中,令y=0,則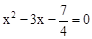 ,整理得,4x2﹣12x﹣7=0,
,整理得,4x2﹣12x﹣7=0,
解得x1=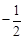 ,x2=
,x2=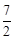 。∴A(
。∴A(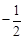 ,0),B(
,0),B(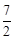 ,0)。
,0)。
在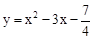 中,令x=0,則y=
中,令x=0,則y= 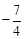 。∴C(0,
。∴C(0,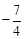 )。
)。
∵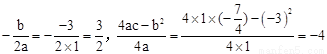 ,∴頂點D(
,∴頂點D(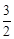 ,﹣4)。
,﹣4)。
(2)在y軸正半軸上存在符合條件的點P。
設點P的坐標為(0,y),
∵A(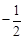 ,0),C(0,
,0),C(0,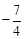 ),∴OA=
),∴OA=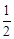 ,OC=
,OC=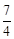 ,OP=y,
,OP=y,
①若OA和OA是對應邊,則△AOP∽△AOC,∴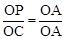 。∴y=OC=
。∴y=OC=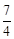 ,此時點P(0,
,此時點P(0,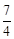 )。
)。
②若OA和OC是對應邊,則△POA∽△AOC,∴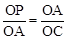 ,即
,即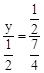 。
。
解得y=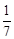 ,此時點P(0,
,此時點P(0,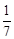 )。
)。
綜上所述,符合條件的點P有兩個,P(0,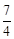 )或(0,
)或(0,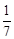 )。
)。
(3)①設直線l的解析式為y=kx+b(k≠0),
∵直線l經過點E(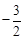 ,0)和點F(0,
,0)和點F(0,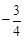 ),
),
∴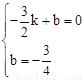 ,解得
,解得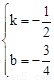 ,
,
∴直線l的解析式為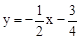 。
。
∵B(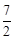 ,0),D(
,0),D(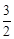 ,﹣4),
,﹣4),
∴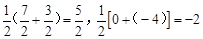 ,∴線段BD的中點G的坐標為(
,∴線段BD的中點G的坐標為(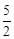 ,﹣2)。
,﹣2)。
當x=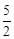 時,
時,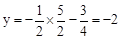 ,∴點G在直線l上。
,∴點G在直線l上。
②在拋物線上存在符合條件的點M。
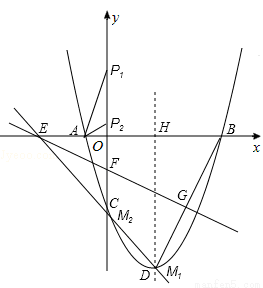
設拋物線的對稱軸與x軸交點為H,則點H的坐標為(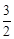 ,0),
,0),
∵E(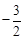 ,0)、F(0,
,0)、F(0,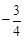 ),B(
),B(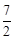 ,0)、D(
,0)、D(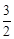 ,﹣4),
,﹣4),
∴OE=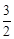 ,OF=
,OF=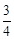 ,HD=4,HB=
,HD=4,HB=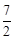 ﹣
﹣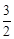 =2。
=2。
∵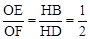 ,∠OEF=∠HDB,
,∠OEF=∠HDB,
∴△OEF∽△HDB。∴∠OFE=∠HBD。
∵∠OEF+∠OFE=90°,∴∠OEF+∠HBD=90°。
∴∠EGB=180°﹣(∠OEF+∠HBD)
=180°﹣90°=90°,
∴直線l是線段BD的垂直平分線。
∴點D關于直線l的對稱點就是點B。
∴點M就是直線DE與拋物線的交點。
設直線DE的解析式為y=mx+n,
∵D(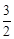 ,﹣4),E(
,﹣4),E(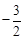 ,0),
,0),
∴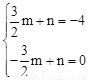 ,解得
,解得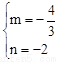 。
。
∴直線DE的解析式為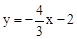 。
。
聯立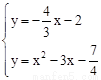 ,解得
,解得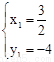 ,
,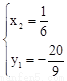 。
。
∴符合條件的點M有兩個,是(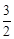 ,﹣4)或(
,﹣4)或(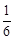 ,
,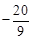 )。
)。
【解析】
試題分析:(1)令y=0,解關于x的一元二次方程求出A、B的坐標,令x=0求出點C的坐標,再根據頂點坐標公式計算即可求出頂點D的坐標。
(2)根據點A、C的坐標求出OA、OC的長,再分OA和OA是對應邊,OA和OC是對應邊兩種情況,利用相似三角形對應邊成比例列式求出OP的長,從而得解。
(3)①設直線l的解析式為y=kx+b(k≠0),利用待定系數法求一次函數解析式求出直線l的解析式,再利用中點公式求出點G的坐標,然后根據直線上點的坐標特征驗證即可。
②設拋物線的對稱軸與x軸交點為H,求出OE、OF、HD、HB的長,然后求出△OEF和△HDB相似,根據相似三角形對應角相等求出∠OFE=∠HBD,然后求出EG⊥BD,從而得到直線l是線段BD的垂直平分線,根據線段垂直平分線的性質點D關于直線l的對稱點就是B,從而判斷出點M就是直線DE與拋物線的交點。再設直線DE的解析式為y=mx+n,利用待定系數法求一次函數解析求出直線DE的解析式,然后與拋物線解析式聯立求解即可得到符合條件的點M。


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com