
【題目】某校計劃購買甲、乙兩種樹苗共1000株用以綠化校園,甲種樹苗每株25元,乙種樹苗每株30元,通過調查了解,甲,乙兩種樹苗成活率分別是90%和95%.
(1)若購買這種樹苗共用去28000元,則甲、乙兩種樹苗各購買多少株?
(2)要使這批樹苗的總成活率不低于92%,則甲種樹苗最多購買多少株?
(3)在(2)的條件下,應如何選購樹苗,使購買樹苗的費用最低?并求出最低費用.
【答案】(1)購甲種樹苗400株,乙種樹苗600株;(2)甲種樹苗最多購買600株;(3)購買家中樹苗600株.乙種樹苗400株時總費用最低,最低費用為27000元.
【解析】試題分析:(1)方程組的應用解題關鍵是設出未知數,找出等量關系,列出方程組求解.本題設購甲種樹苗x株,乙種樹苗y株,根據購買甲、乙兩種樹苗共1000株和購買兩種樹苗的總價為28000元建立方程組求出其解即可.
(2)不等式的應用解題關鍵是找出不等量關系,列出不等式求解.本題設購買甲種樹苗a株,則購買乙種樹苗(1000﹣a)株,由這批樹苗的總成活率不低于92%建立不等式求出其解即可.
(3)設購買樹苗的總費用為W元,根據總費用=兩種樹苗的費用之和建立解析式,由一次函數的性質求出結論.
試題解析:解:(1)設購甲種樹苗x株,乙種樹苗y株,由題意,得
![]() ,解得:
,解得:![]() .
.
答:購甲種樹苗400株,乙種樹苗600株.
(2)設購買甲種樹苗a株,則購買乙種樹苗(1000﹣a)株,由題意,得
90%a+95%(1000﹣a)≥92%×1000,解得:a≤600.
答:甲種樹苗最多購買600株.
(3)設購買樹苗的總費用為W元,由題意,得
W=25a+30(1000﹣a)=﹣5a+30000.
∵k=﹣5<0,∴W隨a的增大而減小,
∵0<a≤600,∴a=600時,W最小=27000元.
∴購買家中樹苗600株.乙種樹苗400株時總費用最低,最低費用為27000元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖是由7個形狀、大小完全相同的正六邊形組成的網格,正六邊形的頂點稱為格點.已知每個正六邊形的邊長為1,△ABC的頂點都在格點上,求△ABC的面積.
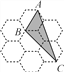
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在Rt△ABC中,∠C=90°,有一內接正方形DEFC,連接AF交DE于G,若AC=15,BC=10.
(1)求正方形DEFC的邊長;(2)求EG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有A、B、C三個居民小區的位置成三角形,現決定在三個小區之間修建一個購物超市,使超市到三個小區的距離相等,則超市應建在( )

A. 在AC、BC兩邊高線的交點處
B. 在AC、BC兩邊中線的交點處
C. 在AC、BC兩邊垂直平分線的交點處
D. 在∠A、∠B兩內角平分線的交點處
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解下列方程:
(1) x2﹣5x﹣6=0;
(2) (1﹣x)2﹣1=![]() ;
;
(3) 8x(x+2)=3x+6;
(4)(y+![]() )(y-
)(y-![]() )=20.
)=20.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系中,點A,B的坐標分別為(-1,0),(3,0),現同時將點A,B分別向上平移2個單位長度,再向右平移1個單位長度,分別得到點A,B的對應點C,D,連接AC,BD,CD.
(1)求點C,D的坐標及S四邊形ABDC.
(2)在y軸上是否存在一點Q,連接QA,QB,使S△QAB=S四邊形ABDC?若存在這樣一點,求出點Q的坐標;若不存在,試說明理由.
(3)如圖②,點P是線段BD上的一個動點,連接PC,PO,當點P在BD上移動時(不與B,D重合),給出下列結論:①![]() 的值不變,②
的值不變,②![]() 的值不變,其中有且只有一個是正確的,請你找出這個結論并求其值.
的值不變,其中有且只有一個是正確的,請你找出這個結論并求其值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)例:代數式(a+b)2表示a、b兩數和的平方.仿照上例填空:
代數式a2﹣b2表示_____.
代數式(a+b)(a﹣b)表示_____.
(2)試計算a、b取不同數值時,a2﹣b2及(a+b)(a﹣b)的植,填入下表:

(3)請你再任意給a、b各取一個數值,并計算a2﹣b2及(a+b)(a﹣b)的植:
當a=_____,b=_____時,a2﹣b2=_____,(a+b)(a﹣b)=_____.
(4)我的發現:_____.
(5)用你發現的規律計算:78.352﹣21.652.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小穎和小紅兩位同學在學習“概率”時,做投擲骰子(質地均勻的正方體)試驗,他們共做了60次試驗,試驗的結果如下:
![]()
(1)計算“3點朝上”的頻率和“5點朝上”的頻率.
(2)小穎說:“根據上述試驗,一次試驗中出現5點朝上的概率最大”;小紅說:“如果投擲600次,那么出現6點朝上的次數正好是100次”.小穎和小紅的說法正確嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com