
【題目】(1)例:代數式(a+b)2表示a、b兩數和的平方.仿照上例填空:
代數式a2﹣b2表示_____.
代數式(a+b)(a﹣b)表示_____.
(2)試計算a、b取不同數值時,a2﹣b2及(a+b)(a﹣b)的植,填入下表:

(3)請你再任意給a、b各取一個數值,并計算a2﹣b2及(a+b)(a﹣b)的植:
當a=_____,b=_____時,a2﹣b2=_____,(a+b)(a﹣b)=_____.
(4)我的發現:_____.
(5)用你發現的規律計算:78.352﹣21.652.
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在四邊形ABCD中,∠D=37°,點E是BC邊上一點,沿AE折疊,點B落在AD上B′處,若B′E∥CD,則∠B=_________°.

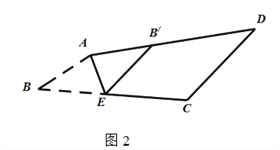
(2)如圖2,在四邊形ABCD中,AB∥CD,點E是BC邊上一點,沿AE折疊,點B落在AD上B′處,點F是BC邊上一點,沿DF折疊,點C落在AD上C′處.B′E與C′F有何位置關系?為什么?
(3)如圖3,在四邊形ABCD中,∠B=∠D=90°,點E是BC邊上一點,沿AE折疊,點B落在AD上B′處,點F是AD邊上一點,沿CF折疊,點D落在BC上D′處.試問:AE與CF有何位置關系?說明理由.

(4)在四邊形ABCD中,點E是BC邊上一點,沿AE折疊.
①若點B落在四邊形ABCD內B′處(如圖4),則∠1,∠2,∠BAD,∠B之間的數量關系為________.
②若點B落在四邊形ABCD外B′處(如圖5),則∠1,∠2,∠BAD,∠B之間的數量關系為 ______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃購買甲、乙兩種樹苗共1000株用以綠化校園,甲種樹苗每株25元,乙種樹苗每株30元,通過調查了解,甲,乙兩種樹苗成活率分別是90%和95%.
(1)若購買這種樹苗共用去28000元,則甲、乙兩種樹苗各購買多少株?
(2)要使這批樹苗的總成活率不低于92%,則甲種樹苗最多購買多少株?
(3)在(2)的條件下,應如何選購樹苗,使購買樹苗的費用最低?并求出最低費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年某區為綠化行車道,計劃購買甲、乙兩種樹苗共計n棵.設購買甲種樹苗x棵,有關甲、乙兩種樹苗的信息如圖所示.
(1)當n=500時,
①根據信息填表(用含x的式子表示);
樹苗類型 | 甲種樹苗 | 乙種樹苗 |
購買樹苗數量(單位:棵) | x | |
購買樹苗的總費用(單位:元) |
②如果購買甲、乙兩種樹苗共用去25 600元,那么甲、乙兩種樹苗各購買了多少棵?
(2)要使這批樹苗的成活率不低于92%,且使購買這兩種樹苗的總費用為26 000元,求n的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖是一個組合幾何體,右邊是它的兩種視圖,在右邊橫線上填寫出兩種視圖的名稱;

視圖 視圖
(2)根據兩種視圖中尺寸(單位:cm),計算這個組合幾何體的表面積.(π取3.14)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個城鎮A、B與兩條公路l1、l2位置如圖所示,電信部門需在C處修建一座信號發射塔,要求發射塔到兩個城鎮A、B的距離必須相等,到兩條公路l1,l2的距離也必須相等,那么點C應選在何處?請在圖中,用尺規作圖找出所有符合條件的點C.(不寫已知、求作、作法,只保留作圖痕跡)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB =AC=2,∠B = 40°,點D在線段BC上運動(不與點B,C重合),連接AD,作∠ADE = 40°,DE交線段AC于點E.
(1)當∠BDA = 115°時,∠BAD= °,∠DEC = °,當點D從點B向點C運動時,∠BDA逐漸變 (填“大”或“小”) .
(2)當DC等于多少時,△ABD≌△DCE?請說明理由.
(3)在點D的運動過程中,是否存在△ADE是等腰三角形?若存在,請直接寫出此時∠BDA的度數;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中.
(1)把![]()
![]() 平移至
平移至![]() 的位置,使點
的位置,使點![]() 與
與![]() 對應,得到
對應,得到![]() ;
;
(2)運用網格畫出![]() 邊上的高
邊上的高![]() 所在的直線,標出垂足
所在的直線,標出垂足![]() ;
;
(3)線段![]() 與
與![]() 的關系是_____________;
的關系是_____________;
(4)如果![]() 是按照先向上4格,再向右5格的方式平移到
是按照先向上4格,再向右5格的方式平移到![]() ,那么線段
,那么線段![]() 在運動過程中掃過的面積是___________.
在運動過程中掃過的面積是___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,AB邊上有一動點P,連接PD,線段PD繞點P順時針旋轉90°后,得到線段PE,且PE交BC于F,連接DF,過點E作EQ⊥AB的延長線于點Q.
(1)求線段PQ的長;
(2)問:點P在何處時,△PFD∽△BFP,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com