
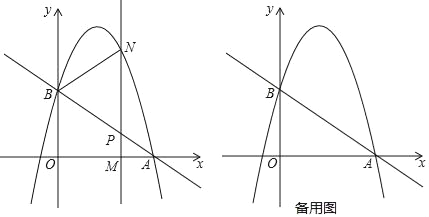
【題目】如圖,直線y=﹣![]() x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣
x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣![]() x2+bx+c經過點A,B.
x2+bx+c經過點A,B.
(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N.
①點M在線段OA上運動,若以B,P,N為頂點的三角形與△APM相似,求點M的坐標;
②點M在x軸上自由運動,若三個點M,P,N中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱M,P,N三點為“共諧點”.請直接寫出使得M,P,N三點成為“共諧點”的m的值.
【答案】(1)拋物線解析式為y=﹣![]() x2+
x2+![]() x+2;(2)①點M的坐標為(2.5,0)或(
x+2;(2)①點M的坐標為(2.5,0)或(![]() ,0);②m的值為
,0);②m的值為![]() 或﹣1或﹣
或﹣1或﹣![]() .
.
【解析】試題分析:(1)把A點坐標代入直線解析式可求得c,則可求得B點坐標,由A、B的坐標,利用待定系數法可求得拋物線解析式;
(2)①由M點坐標可表示P、N的坐標,從而可表示出MA、MP、PN、PB的長,分∠NBP=90°和∠BNP=90°兩種情況,分別利用相似三角形的性質可得到關于m的方程,可求得m的值;
②用m可表示出M、P、N的坐標,由題意可知有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點,可分別得到關于m的方程,可求得m的值.
試題解析:解:
(1)∵![]() 與x軸交于點A(3,0),與y軸交于點B,∴0=﹣2+c,解得c=2,∴B(0,2),∵拋物線
與x軸交于點A(3,0),與y軸交于點B,∴0=﹣2+c,解得c=2,∴B(0,2),∵拋物線![]() 經過點A,B,∴
經過點A,B,∴![]() ,解得:
,解得: 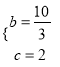 ,∴拋物線解析式為
,∴拋物線解析式為![]() ;
;
(2)①由(1)可知直線解析式為![]() ,∵M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N,∴P(m,
,∵M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N,∴P(m, ![]() ),N(m,
),N(m, ![]() ),∴PM=
),∴PM=![]() ,PA=3﹣m,PN=
,PA=3﹣m,PN=![]() ﹣(
﹣(![]() )=
)=![]() ,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,分兩種情況:
,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,分兩種情況:
當∠BNP=90°時,則有BN⊥MN,∴點N的縱坐標為2,∴ ![]() =2,解得m=0(舍去)或m=
=2,解得m=0(舍去)或m=![]() ,∴M(
,∴M(![]() ,0);
,0);
當∠NBP=90°時,則有![]() ,∵A(3,0),B(0,2),P(m,
,∵A(3,0),B(0,2),P(m, ![]() ),∴BP=
),∴BP=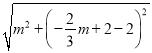 =
= ![]() ,AP=
,AP=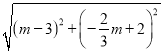 =
=![]() (3﹣m),∴
(3﹣m),∴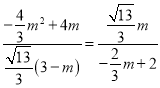 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m=![]() ,∴M(
,∴M(![]() ,0);
,0);
綜上可知當以B,P,N為頂點的三角形與△APM相似時,點M的坐標為(![]() ,0)或(
,0)或(![]() ,0);
,0);
②由①可知M(m,0),P(m, ![]() ),N(m,
),N(m, ![]() ),∵M,P,N三點為“共諧點”,∴有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點,當P為線段MN的中點時,則有2(
),∵M,P,N三點為“共諧點”,∴有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點,當P為線段MN的中點時,則有2(![]() )=
)=![]() ,解得m=3(三點重合,舍去)或m=
,解得m=3(三點重合,舍去)或m=![]() ;
;
當M為線段PN的中點時,則有![]() +(
+(![]() )=0,解得m=3(舍去)或m=﹣1;
)=0,解得m=3(舍去)或m=﹣1;
當N為線段PM的中點時,則有![]() =2(
=2(![]() ),解得m=3(舍去)或m=
),解得m=3(舍去)或m=![]() ;
;
綜上可知當M,P,N三點成為“共諧點”時m的值為![]() 或﹣1或
或﹣1或![]() .
.


科目:初中數學 來源: 題型:
【題目】有依次排列的3個數:6,2,8,先將任意相鄰的兩個數,都用右邊減去左邊的數,所得之差寫在這兩個數之間,可產生一個新的數串:6,-4,2,6,8這稱為第一次操作;做第二次同樣操作后也可產生一個新數串:6,-10,-4,6,2,4,6,2,8,繼續依次操作下去,問:從數串中6,2,8開始操作第2019次后所產生的那個新數串的所有數之和是( )
A.4054B.4056C.4058D.4060
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王上周買進某種股票1000股,每股27元。

(1)星期三收盤時,每股是多少元?
(2)本周內最高價是每股多少元?最低價是每股多少元?
(3)若小王在本周五的收盤價將股票全部賣出,你認為他會獲利嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,![]() 三點在同一直線上,
三點在同一直線上,![]() .
.
(1)已知點![]() 在直線
在直線![]() 上,根據條件,請補充完整圖形,并求
上,根據條件,請補充完整圖形,并求![]() 的長;
的長;
![]()
(2)已知點![]() 在直線
在直線![]() 上,
上,![]() 分別是
分別是![]() ,
,![]() 的中點,根據條件,請補充完整圖形,并求
的中點,根據條件,請補充完整圖形,并求![]() 的長,直接寫出
的長,直接寫出![]() 與
與![]() 的長存在的數量關系;
的長存在的數量關系;
![]()
(3)已知點![]() 在直線
在直線![]() 上,
上,![]() 分別是
分別是![]() ,
,![]() 的中點,根據條件,請補充完整圖形,并求
的中點,根據條件,請補充完整圖形,并求![]() 的長,直接寫出
的長,直接寫出![]() 與
與![]() 的長存在的數量關系.
的長存在的數量關系.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數y=![]() 為反比例函數.
為反比例函數.
(1)求k的值;
(2)它的圖象在第 象限內,在各象限內,y隨x增大而 ;(填變化情況)
(3)求出﹣2≤x≤﹣![]() 時,y的取值范圍.
時,y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有![]() 、
、![]() 、
、![]() 三個居民小區的位置成三角形,現決定在三個小區之間修建一個購物超市,使超市到三個小區的距離相等,則超市應建在( )
三個居民小區的位置成三角形,現決定在三個小區之間修建一個購物超市,使超市到三個小區的距離相等,則超市應建在( )
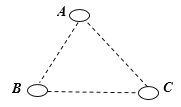
A.在∠A、∠B兩內角平分線的交點處
B.在AC、BC兩邊垂直平分線的交點處
C.在AC、BC兩邊高線的交點處
D.在AC、BC兩邊中線的交點處
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△BAD是由△BEC在平面內繞點B旋轉60°而得,且AB⊥BC,BE=CE,連接DE.
(1)求證:△BDE≌△BCE;
(2)試判斷四邊形ABED的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算下列各題:
(1)(-12.5)+20.5;
(2)2![]() ×(-
×(-![]() );
);
(3)10+2÷![]() ×(-2);
×(-2);
(4)1-(1-0.5)×![]() ×[2-(-2)2];
×[2-(-2)2];
(5)-52+(-2)÷![]() 2;
2;
(6)-22÷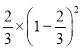 ;
;
(7)17-23÷(-2)×3;
(8)2×(-5)+23-3÷![]() ;
;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,A是雙曲線![]() 在第一象限的分支上的一個動點,連接AO并延長與這個雙曲線的另一分支交于點B,以AB為底邊作等腰直角三角形ABC,使得點C位于第四象限。
在第一象限的分支上的一個動點,連接AO并延長與這個雙曲線的另一分支交于點B,以AB為底邊作等腰直角三角形ABC,使得點C位于第四象限。
(1)點C與原點O的最短距離是________;
(2)沒點C的坐標為(![]()
![]() ,點A在運動的過程中,y隨x的變化而變化,y關于x的函數關系式為________。
,點A在運動的過程中,y隨x的變化而變化,y關于x的函數關系式為________。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com