
【題目】在平面直角坐標(biāo)系中,我們定義:橫坐標(biāo)與縱坐標(biāo)均為整數(shù)的點(diǎn)為整點(diǎn)如圖,已知雙曲線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,記雙曲線與兩坐標(biāo)軸之間的部分為
,記雙曲線與兩坐標(biāo)軸之間的部分為![]() (不含雙曲線與坐標(biāo)軸).
(不含雙曲線與坐標(biāo)軸).
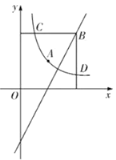
(1)求![]() 的值;
的值;
(2)求![]() 內(nèi)整點(diǎn)的個數(shù);
內(nèi)整點(diǎn)的個數(shù);
(3)設(shè)點(diǎn)![]() 在直線
在直線![]() 上,過點(diǎn)
上,過點(diǎn)![]() 分別作平行于
分別作平行于![]() 軸
軸![]() 軸的直線,交雙曲線
軸的直線,交雙曲線![]()
![]() 于點(diǎn)
于點(diǎn)![]() ,記線段
,記線段![]() 、雙曲線所圍成的區(qū)域?yàn)?/span>
、雙曲線所圍成的區(qū)域?yàn)?/span>![]() ,若
,若![]() 內(nèi)部(不包括邊界)不超過
內(nèi)部(不包括邊界)不超過![]() 個整點(diǎn),求
個整點(diǎn),求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 內(nèi)整點(diǎn)的個數(shù)為
內(nèi)整點(diǎn)的個數(shù)為![]() 個;(3)若
個;(3)若![]() 內(nèi)部(不包括邊界)不超過
內(nèi)部(不包括邊界)不超過![]() 個整點(diǎn),
個整點(diǎn),![]()
【解析】
(1)利用待定系數(shù)法即可求解;
(2)將G內(nèi)x=1,2,3,4分別代入雙曲線,即可求出整點(diǎn);
(3)根據(jù)m的情況進(jìn)行分類討論,具體見解析.
(1)∵![]() 經(jīng)過點(diǎn)A(2,2),
經(jīng)過點(diǎn)A(2,2),
∴![]() ,
,
∴![]() ,
,
(2)對于雙曲線![]() ,
,
當(dāng)![]() 時,
時,![]() ,
,
![]() 在直線
在直線![]() 上,當(dāng)0
上,當(dāng)0![]() 時,有整點(diǎn)(1,1)、(1,2)、(1,3),
時,有整點(diǎn)(1,1)、(1,2)、(1,3),
當(dāng)![]() 時,
時,![]() ,
,
![]() 在直線
在直線![]() 上,當(dāng)0
上,當(dāng)0![]() 時,有整點(diǎn)(2,1),
時,有整點(diǎn)(2,1),
當(dāng)![]() 時,
時,![]() ,
,
![]() 在直線
在直線![]() 上,當(dāng)0
上,當(dāng)0![]() 時,有整點(diǎn)(3,1),
時,有整點(diǎn)(3,1),
當(dāng)![]() 時,
時,![]() ,
,
![]() 在直線
在直線![]() 上,當(dāng)0
上,當(dāng)0![]() 時,沒有整點(diǎn).
時,沒有整點(diǎn).
∴G內(nèi)整點(diǎn)的個數(shù)為5個.
(3)如圖,當(dāng)![]() 時,點(diǎn)B(4,4), 點(diǎn)C(1,4)此時在區(qū)域W內(nèi)(不包含邊界)有(2,3)、(3,2)、(3,3)共3個整點(diǎn),線段BD上有4個整點(diǎn),線段BC上有4個整點(diǎn),
時,點(diǎn)B(4,4), 點(diǎn)C(1,4)此時在區(qū)域W內(nèi)(不包含邊界)有(2,3)、(3,2)、(3,3)共3個整點(diǎn),線段BD上有4個整點(diǎn),線段BC上有4個整點(diǎn),
∵點(diǎn)(4,4)重合,點(diǎn)(4,1)(1,4)在邊界上,
∴當(dāng)![]() 時,區(qū)域W內(nèi)至少有3+4+4-3=8個整點(diǎn),
時,區(qū)域W內(nèi)至少有3+4+4-3=8個整點(diǎn),
當(dāng)![]() 時,B'(4.5,5),C(
時,B'(4.5,5),C(![]() ),
),
線段B'C'上有4個整點(diǎn),此時區(qū)域W內(nèi)整點(diǎn)個數(shù)為8個,
當(dāng)![]() 時,區(qū)域W內(nèi)部整點(diǎn)個數(shù)增加,
時,區(qū)域W內(nèi)部整點(diǎn)個數(shù)增加,
![]() 若W內(nèi)部(不包括邊界)不超過8個整點(diǎn),
若W內(nèi)部(不包括邊界)不超過8個整點(diǎn),![]() .
.



 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一個直角三角形紙片![]() ,放置在平面直角坐標(biāo)系中,點(diǎn)
,放置在平面直角坐標(biāo)系中,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]()
(I)過邊![]() 上的動點(diǎn)
上的動點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,沿著
,沿著![]() 折疊該紙片,點(diǎn)
折疊該紙片,點(diǎn)![]() 落在射線
落在射線![]() 上的點(diǎn)
上的點(diǎn)![]() 處.
處.
①如圖,當(dāng)![]() 為
為![]() 中點(diǎn)時,求
中點(diǎn)時,求![]() 點(diǎn)的坐標(biāo);
點(diǎn)的坐標(biāo);
②連接![]() ,當(dāng)
,當(dāng)![]() 為直角三角形時,求
為直角三角形時,求![]() 點(diǎn)坐標(biāo):
點(diǎn)坐標(biāo):
(Ⅱ)![]() 是
是![]() 邊上的動點(diǎn)(點(diǎn)
邊上的動點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合),將
重合),將![]() 沿
沿![]() 所在的直線折疊,得到
所在的直線折疊,得到![]() ,連接
,連接![]() ,當(dāng)
,當(dāng)![]() 取得最小值時,求
取得最小值時,求![]() 點(diǎn)坐標(biāo)(直接寫出結(jié)果即可).
點(diǎn)坐標(biāo)(直接寫出結(jié)果即可).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中, ![]() 是直線
是直線![]() 上的一點(diǎn),連接
上的一點(diǎn),連接![]() 過點(diǎn)
過點(diǎn)![]() 作
作![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() .
.
![]() 當(dāng)點(diǎn)
當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時,如圖①,求證:
上時,如圖①,求證:![]() ;
;
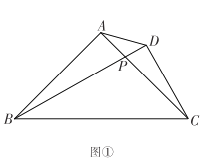
![]() 當(dāng)點(diǎn)
當(dāng)點(diǎn)![]() 在直線
在直線![]() 上移動時,位置如圖②、圖③所示,線段
上移動時,位置如圖②、圖③所示,線段![]() 與
與![]() 之間又有怎樣的數(shù)量關(guān)系?請直接寫出你的猜想,不需證明.
之間又有怎樣的數(shù)量關(guān)系?請直接寫出你的猜想,不需證明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
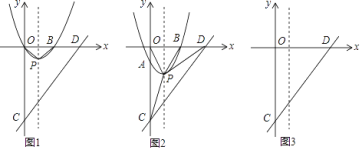
【題目】如圖,平面直角坐標(biāo)系中,拋物線y=x2﹣2x與x軸交于O、B兩點(diǎn),頂點(diǎn)為P,連接OP、BP,直線y=x﹣4與y軸交于點(diǎn)C,與x軸交于點(diǎn)D.
(1)寫出點(diǎn)B坐標(biāo);判斷△OBP的形狀;
(2)將拋物線沿對稱軸平移m個單位長度,平移的過程中交y軸于點(diǎn)A,分別連接CP、DP;
(i)若拋物線向下平移m個單位長度,當(dāng)S△PCD= ![]() S△POC時,求平移后的拋物線的頂點(diǎn)坐標(biāo);
S△POC時,求平移后的拋物線的頂點(diǎn)坐標(biāo);
(ii)在平移過程中,試探究S△PCD和S△POD之間的數(shù)量關(guān)系,直接寫出它們之間的數(shù)量關(guān)系及對應(yīng)的m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于題目:在平面直角坐標(biāo)系中,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于
軸交于![]() 兩點(diǎn),過點(diǎn)
兩點(diǎn),過點(diǎn)![]() 且平行
且平行![]() 軸的直線與過點(diǎn)
軸的直線與過點(diǎn)![]() 且平行
且平行![]() 軸的直線相交于點(diǎn)
軸的直線相交于點(diǎn)![]() ,若拋物線
,若拋物線![]() 與線段
與線段![]() 有唯一公共點(diǎn),求
有唯一公共點(diǎn),求![]() 的取值范圍.甲的計(jì)算結(jié)果是
的取值范圍.甲的計(jì)算結(jié)果是![]() ;乙的計(jì)算結(jié)果是
;乙的計(jì)算結(jié)果是![]() ,則( )
,則( )
A.甲的結(jié)果正確B.乙的結(jié)果正確
C.甲與乙的結(jié)果合在一起正確D.甲與乙的結(jié)果合在一起也不正確
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
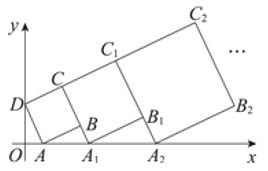
【題目】在平面直角坐標(biāo)系中,正方形![]() 的位置如圖所示,點(diǎn)
的位置如圖所示,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,延長
,延長![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,作正方形
,作正方形![]() ;延長
;延長![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,作正方形
,作正方形![]() ;…,按照這樣的規(guī)律作正方形,則點(diǎn)
;…,按照這樣的規(guī)律作正方形,則點(diǎn)![]() 的縱坐標(biāo)為__________.
的縱坐標(biāo)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校九年級( 3 )班全體學(xué)生 2019 年初中畢業(yè)體育考試的成績統(tǒng)計(jì)如下表:
成績 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人數(shù) | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根據(jù)上表中的信息判斷,下列結(jié)論中錯誤的是 ( )
A.該班一共有 40 名同學(xué)B.該班學(xué)生這次考試成績的眾數(shù)是 45 分
C.該班學(xué)生這次考試成績的中位數(shù)是 44 分D.該班學(xué)生這次考試成績的平均數(shù)是 45 分
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△BCE中,點(diǎn)A是邊BE上一點(diǎn),以AB為直徑的⊙O與CE相切于點(diǎn)D,AD∥OC,點(diǎn)F為OC與⊙O的交點(diǎn),連接AF.
(1)求證:CB是⊙O的切線;
(2)若∠ECB=60°,AB=6,求圖中陰影部分的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
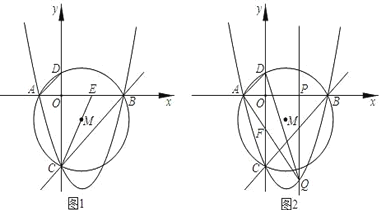
【題目】如圖1,已知拋物線y=ax2﹣2x+c(a≠0)與x軸交于A、B兩點(diǎn)(A點(diǎn)在B點(diǎn)左側(cè)),與y軸交于點(diǎn)C(0,﹣3),對稱軸是直線x=1,△ACB的外接圓M交y軸的正半軸與點(diǎn)D,連結(jié)AD、CM,并延長CM交x軸于點(diǎn)E.
(1)求拋物線的函數(shù)表達(dá)式和直線BC的函數(shù)表達(dá)式;
(2)求證:△CAD∽△CEB;
(3)如圖2,P為x軸正半軸上的一個動點(diǎn),OP=t,(0<t<3),過P點(diǎn)與y軸平行的直線交拋物線與點(diǎn)Q,若△QAD的面積為S,寫出S與t的函數(shù)表達(dá)式,問:當(dāng)t為何值時,△QAD的面積最大,且最大面積為多少?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com