【題目】計算：（﹣10）﹣（﹣2）+（﹣6）﹣11
科目：初中數學 來源： 題型：
【題目】《九章算術》是中國古代的數學專著，奠定了中國傳統數學的基本框架．它的代數成就主要包括開方術、正負術和方程術．其中，方程術是《九章算術》最高的數學成就．《九章算術》中記載：“今有共買羊，人出五，不足四十五；人出七，不足三．問人數、羊價各幾何？”譯文：“假設有若干人共同出錢買羊，如果每人出5錢，那么還差45錢；如果每人出7錢那么仍舊差3錢，求買羊的人數和羊的價錢．”設共有x個人買羊，可列方程為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小紅和小明在研究一個數學問題：已知AB∥CD，AB和CD都不經過點E，探索∠E與∠A，∠C的數量關系． 
（1）發現：在圖1中，小紅和小明都發現：∠AEC=∠A+∠C； 小紅是這樣證明的：如圖7過點E作EQ∥AB．
∴∠AEQ=∠A（）
∵EQ∥AB，AB∥CD．
∴EQ∥CD（）
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C．
小明是這樣證明的：如圖7過點E作EQ∥AB∥CD．
∴∠AEQ=∠A，∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
請在上面證明過程的橫線上，填寫依據：
兩人的證明過程中，完全正確的是 ．
（2）嘗試： ①在圖2中，若∠A=110°，∠C=130°，則∠E的度數為；
②在圖3中，若∠A=20°，∠C=50°，則∠E的度數為 ．
（3）探索： 裝置圖4中，探索∠E與∠A，∠C的數量關系，并說明理由．
（4）猜想： 如圖5，∠B、∠D、∠E、∠F、∠G之間有什么關系？（直接寫出結論）
（5）如圖6，你可以得到什么結論？（直接寫出結論）
查看答案和解析>>
科目：初中數學 來源： 題型：
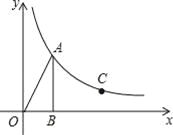
【題目】如圖，在平面直角坐標系中，Rt△OAB的頂點B在x軸的正半軸上，已知∠OBA=90°，OB=3，sin∠AOB=
．反比例函數y=
（x＞0）的圖象經過點A．
（1）求反比例函數的解析式；
（2）若點C（m，2）是反比例函數y=
（x＞0）圖象上的點，則在x軸上是否存在點P，使得PA+PC最小？若存在，求出點P的坐標；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
