
【題目】如圖,將弧BC沿弦BC折疊交直徑AB于點D,若AD=2,DB=3,則BC的長是_______.

【答案】![]()
【解析】
根據折疊的性質可得弧BC等于弧BDC,再根據在同圓或等圓中,等弧所對的圓周角相等可得∠BAC=∠BCD+∠CBD,根據三角形的一個外角等于與它不相鄰的兩個內角的和可得∠ADC=∠BCD+∠CBD,從而得到∠BAC=∠ADC,根據等角對等邊可得AC=CD,過點C作CE⊥AD于E,根據等腰三角形三線合一的性質可得AE=DE=![]() AD,然后利用△ACE和△CBE相似,根據相似三角形對應邊成比例列式求出CE,在Rt△BCE中,利用勾股定理列式計算即可得解.
AD,然后利用△ACE和△CBE相似,根據相似三角形對應邊成比例列式求出CE,在Rt△BCE中,利用勾股定理列式計算即可得解.
∵弧BC沿弦BC折疊交直徑AB于點D,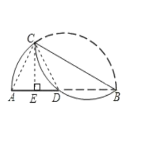
∴弧BC等于弧BDC,
∴∠BAC=∠BCD+∠CBD,
在△BCD中,∠ADC=∠BCD+∠CBD,
∴∠BAC=∠ADC,
∴AC=CD,
過點C作CE⊥AD于E,
則AE=DE=![]() AD=
AD=![]() ×2=1,
×2=1,
∴BE=BD+DE=3+1=4,
∵AB是直徑,
∴∠ACB=90°,
∴∠ACE+∠BCE=∠ACB=90°,
∵∠ACE+∠CAE=180°-90°=90°,
∴∠CAE=∠BCE,
又∵∠AEC=∠BEC=90°,
∴△ACE∽△CBE,
∴![]() =
=![]() ,
,
∴CE2=AEBE,
∴CE=2
在Rt△BCE中,BC2=4+16=20
BC=![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列五個命題:![]() 兩個端點能夠重合的弧是等弧;
兩個端點能夠重合的弧是等弧;![]() 圓的任意一條弧必定把圓分成劣弧和優弧兩部分
圓的任意一條弧必定把圓分成劣弧和優弧兩部分![]() 經過平面上任意三點可作一個圓;
經過平面上任意三點可作一個圓;![]() 任意一個圓有且只有一個內接三角形
任意一個圓有且只有一個內接三角形![]() 三角形的外心到各頂點距離相等.其中真命題有( )
三角形的外心到各頂點距離相等.其中真命題有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
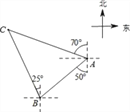
【題目】如圖,輪船在A處觀測燈塔C位于北偏西70°方向上,輪船從A處以每小時20海里的速度沿南偏西50°方向勻速航行,1小時后到達碼頭B處,此時,觀測燈塔C位于北偏西25°方向上,則燈塔C與碼頭B的距離是( )
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四張背面完全相同的紙牌A、B、C、D,其中正面分別畫有四個不同的幾何圖形(如圖),小華將這4張紙牌背面朝上洗勻后摸出一張,放回洗勻后再摸一張.
(1)用樹狀圖(或列表法)表示兩次摸牌所有可能出現的結果(紙牌可用A、B、C、D表示);
(2)求摸出兩張紙牌牌面上所畫幾何圖形,既是軸對稱圖形又是中心對稱圖形的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
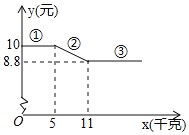
【題目】某水果店進行了一次水果促銷活動,在該店一次性購買A種水果的單價y(元)與購買量x(千克)的函數關系如圖所示,
(1)當0<x≤5時,單價y為 元.當單價y=8.8時,x的取值范圍為 .
(2)根據函數圖象,求第②段函數圖象中單價y(元)與購買量(千克)的函數關系式,并寫出x的取值范圍.
(3)促銷活動期間,張老師計劃去該店購買A種水果10千克,那么張老師共需花費多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 在![]() .
.
(1)用尺規作圖方法,按要求作圖:
①作![]() 的高
的高![]() ;
;
②作![]() 的平分線
的平分線![]() ,分別交
,分別交![]() 于點
于點![]() ;
;
(要求:保留作圖痕跡,不寫作法和證明)
(2)求證:點![]() 在
在![]() 的垂直平分線.上; .
的垂直平分線.上; .
(3)在(1)所作的圖中,探究線段AE與BF的數量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
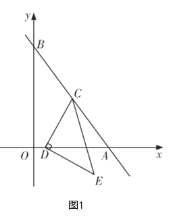
【題目】如圖1,在平面直角坐標系![]() 中,直線
中,直線![]() 分別交
分別交![]() 軸,
軸,![]() 軸于
軸于![]() 、
、![]() 兩點,已知
兩點,已知![]() 點坐標
點坐標![]() ,點
,點![]() 在直線
在直線![]() 上,橫坐標為
上,橫坐標為![]() ,點
,點![]() 是
是![]() 軸正半軸上的一個動點,連結
軸正半軸上的一個動點,連結![]() ,以
,以![]() 為直角邊在右側構造一個等腰
為直角邊在右側構造一個等腰![]() ,且
,且![]() .
.

(1)求直線![]() 的解析式以及
的解析式以及![]() 點坐標;
點坐標;
(2)設點![]() 的橫坐標為
的橫坐標為![]() ,試用含
,試用含![]() 的代數式表示點
的代數式表示點![]() 的坐標;
的坐標;
(3)如圖2,連結![]() ,
,![]() ,請直接寫出使得
,請直接寫出使得![]() 周長最小時,點
周長最小時,點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一座鋼結構橋梁的框架是△ABC,水平橫梁BC長18米,中柱AD高6米,其中D是BC的中點,且AD⊥BC.
(1)求sinB的值;
(2)現需要加裝支架DE、EF,其中點E在AB上,BE=2AE,且EF⊥BC,垂足為點F,求支架DE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com