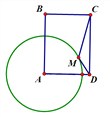
【題目】如圖，已知矩形ABCD，AB=8，BC=6，以點A為圓心，5為半徑作圓，點M為圓A上一動點，連接CM，DM,則
CM+MD的最小值為_________．
【答案】
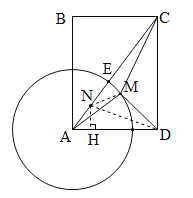
【解析】分析：連接AC交⊙A于點E，取AE的中點N，連接MN，ND，則
CM+DM的最小值就是DN的長．作NH⊥AD，易求NH，AH，HD的長．在Rt△NHD中，由勾股定理即可得出結論．
詳解：連接AC交⊙A于點E，取AE的中點N，連接MN，ND，則CM+DM的最小值就是DN的長．理由如下：
易知AC=
=
=10，AM=5，AN=2.5，
∴
．
∵∠MAN=∠CAM（公共角），∴△MAN∽△CAM，∴
，即MN=MC，
∴MC+DM=MN+DM≥DN，當N、M、D三點共線時等號成立．即CM+DM的最小值就是DN的長．
作NH⊥AD，易求NH=2.5×
=2，AH=2.5×
=1.5，HD=AD-AH=6-1.5=4.5，
∴ND=
=
=．
故答案為：．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】把下列各數填入對應的橫線內：
－38，4.8，+84，3.1416，0，2008，－
，－0.142，95%，+
．
非負整數：______________________________________________________________
負整數：______________________________________________________________
正分數：_____________________________________________________________
負有理數：______________________________________________________________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形
的頂點
、
分別在
、
軸的正半軸上，點
為
邊上的點， 
，反比例函數
在第一象限內的圖象經過點
和
邊上的點
.
(1)求
、
的值和反比例函數的表達式.
(2)將矩形
的一角折疊，使點
與點
重合，折痕分別與
軸， 
軸正半軸交于點
，求線段
的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知AB//CD，點C在點D的右側，∠ABC，∠ADC的平分線交于點E(不與B，D點重合).
，
.
(1)若點B在點A的左側，求∠BED的度數(用含
的代數式表示).
(2)將線段BC沿DC方向平移，當點B移動到點A右側時，請畫出圖形并判斷
的度數是否改變.若改變，請求出的度數(用含的代數式表示)；若不變，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
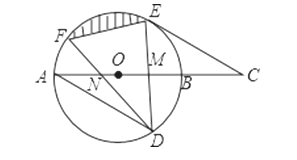
【題目】如圖，AB是⊙O的直徑，弦DE垂直平分半徑OB，垂足為M，DE=4，連接AD，過E作AD平行線交AB延長線于點C．
（1）求⊙O的半徑；
（2）求證：CE是⊙O的切線；
（3）若弦DF與直徑AB交于點N，當∠DNB=30°時，求圖中陰影部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，過點A（2，0）的兩條直線
，
分別交軸于B，C，其中點B在原點上方，點C在原點下方，已知AB=
.
（1）求點B的坐標；
（2）若△ABC的面積為4，求的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
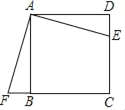
【題目】四邊形ABCD是正方形，E、F分別是DC和CB的延長線上的點，且DE=BF，連接AE、AF、EF．
（1）求證：△ADE≌△ABF．
（2）填空：△ABF可以由△ADE繞旋轉中心 點，按順時針方向旋轉 度得到．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
