
【題目】如圖1,四邊形ABCD的對角線AC,BD相交于點O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.
(1)填空:∠BAD與∠ACB的數量關系為;
(2)求 ![]() 的值;
的值;
(3)將△ACD沿CD翻折,得到△A′CD(如圖2),連接BA′,與CD相交于點P.若CD= ![]() ,求PC的長.
,求PC的長.
【答案】
(1)∠BAD+∠ACB=180°
(2)
解:如圖1中,作DE∥AB交AC于E.
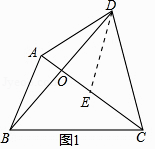
∴∠DEA=∠BAE,∠OBA=∠ODE,
∵OB=OD,
∴△OAB≌△OED,
∴AB=DE,OA=OE,設AB=DE=CE=CE=x,OA=OE=y,
∵∠EDA+∠DAB=180°,∠BAD+∠ACB=180°,
∴∠EDA=∠ACB,
∵∠DEA=∠CAB,
∴△EAD∽△ABC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴4y2+2xy﹣x2=0,
∴( ![]() )2+
)2+ ![]() ﹣1=0,
﹣1=0,
∴ ![]() =
= ![]() (負根已經舍棄),
(負根已經舍棄),
∴ ![]() =
= ![]() .
.
(3)
解:如圖2中,作DE∥AB交AC于E.
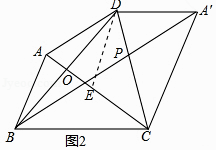
由(1)可知,DE=CE,∠DCA=∠DCA′,
∴∠EDC=∠ECD=∠DCA′,
∴DE∥CA′∥AB,
∴∠ABC+∠A′CB=180°,
∵△EAD∽△ACB,
∴∠DAE=∠ABC=∠DA′C,
∴∠DA′C+∠A′CB=180°,
∴A′D∥BC,
∴△PA′D∽△PBC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
∵CD= ![]() ,
,
∴PC=1.
【解析】解:(1.)如圖1中,
在△ABD中,∵∠BAD+∠ABD+∠ADB=180°,
又∵∠ABD+∠ADB=∠ACB,
∴∠BAD+∠ACB=180°,
【考點精析】根據題目的已知條件,利用相似三角形的判定與性質的相關知識可以得到問題的答案,需要掌握相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D為AC上一點,且CD=CB,以BC為直徑作⊙O,交BD于點E,連接CE,過D作DF⊥AB于點F,∠BCD=2∠ABD. 
(1)求證:AB是⊙O的切線;
(2)若∠A=60°,DF= ![]() ,求⊙O的直徑BC的長.
,求⊙O的直徑BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明隨機調查了若干市民租用共享單車的騎車時間t(單位:分),將獲得的數據分成四組,繪制了如下統計圖(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根據圖中信息,解答下列問題: 
(1)這項被調查的總人數是多少人?
(2)試求表示A組的扇形統計圖的圓心角的度數,補全條形統計圖;
(3)如果小明想從D組的甲、乙、丙、丁四人中隨機選擇兩人了解平時租用共享單車情況,請用列表或畫樹狀圖的方法求出恰好選中甲的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y= ![]() (k為常數).
(k為常數).
(1)若點P1( ![]() ,y1)和點P2(﹣
,y1)和點P2(﹣ ![]() ,y2)是該反比例函數圖象上的兩點,試利用反比例函數的性質比較y1和y2的大小;
,y2)是該反比例函數圖象上的兩點,試利用反比例函數的性質比較y1和y2的大小;
(2)設點P(m,n)(m>0)是其圖象上的一點,過點P作PM⊥x軸于點M.若tan∠POM=2,PO= ![]() (O為坐標原點),求k的值,并直接寫出不等式kx+
(O為坐標原點),求k的值,并直接寫出不等式kx+ ![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解全校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,隨機選取該校部分學生進行調查,要求每名學生從中只選出一類最喜愛的電視節目,以下是根據調查結果繪制的統計圖表的一部分.
類別 | A | B | C | D | E |
節目類型 | 新聞 | 體育 | 動畫 | 娛樂 | 戲曲 |
人數 | 12 | 30 | m | 54 | 9 |

請你根據以上的信息,回答下列問題:
(1)被調查學生中,最喜愛體育節目的有人,這些學生數占被調查總人數的百分比為%.
(2)被調查學生的總數為人,統計表中m的值為 , 統計圖中n的值為 .
(3)在統計圖中,E類所對應扇形的圓心角的度數為 .
(4)該校共有2000名學生,根據調查結果,估計該校最喜愛新聞節目的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛轎車從甲城駛往乙城,同時一輛卡車從乙城駛往甲城,兩車沿相同路線勻速行駛,轎車到達乙城停留一段時間后,按原路原速返回甲城;卡車到達甲城比轎車返回甲城早0.5小時,轎車比卡車每小時多行駛60千米,兩車到達甲城弧均停止行駛,兩車之間的路程y(千米)與轎車行駛時間t(小時)的函數圖象如圖所示,請結合圖象提供的信息解答下列問題: 
(1)請直接寫出甲城和乙城之間的路程,并求出轎車和卡車的速度;
(2)求轎車在乙城停留的時間,并直接寫出點D的坐標;
(3)請直接寫出轎車從乙城返回甲城過程中離甲城的路程s(千米)與轎車行駛時間t(小時)之間的函數關系式(不要求寫出自變量的取值范圍).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D點,E,F分別是AD,AC上的動點,則CE+EF的最小值為( )
A.![]()
B.![]()
C.![]()
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題是真命題的是( )
A.若一組數據是1,2,3,4,5,則它的方差是3
B.若分式方程 ![]() 有增根,則它的增根是1
有增根,則它的增根是1
C.對角線互相垂直的四邊形,順次連接它的四邊中點所得四邊形是矩形
D.若一個角的兩邊分別與另一個角的兩邊平行,則這兩個角相等
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com