
【題目】如圖,以△ABC的各邊,在邊BC的同側分別作三個正方形ABDI,BCFE,ACHG.
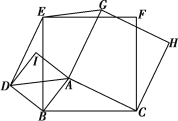
(1)求證:△BDE≌△BAC;
(2)求證:四邊形ADEG是平行四邊形.
(3)直接回答下面兩個問題,不必證明:
①當△ABC滿足條件_____________________時,四邊形ADEG是矩形.
②當△ABC滿足條件_____________________時,四邊形ADEG是正方形?
【答案】(1)見解析;(2)見解析;(3)①∠BAC=135°;②∠BAC=135°且AC=![]()
【解析】
(1)根據全等三角形的判定定理SAS證得△BDE≌△BAC;
(2)由△BDE≌△BAC,可得全等三角形的對應邊DE=AG.然后利用正方形對角線的性質、周角的定義推知∠EDA+∠DAG=180°,易證ED∥GA;最后由“一組對邊平行且相等”的判定定理證得結論;
(3)①根據“矩形的內角都是直角”易證∠DAG=90°.然后由周角的定義求得∠BAC=135°;
②由“正方形的內角都是直角,四條邊都相等”易證∠DAG=90°,且AG=AD.由正方形ABDI和正方形ACHG的性質證得:AC![]() AB.
AB.
(1)∵四邊形ABDI、四邊形BCFE、四邊形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°,∴∠ABC=∠EBD(同為∠EBA的余角).
在△BDE和△BAC中,∵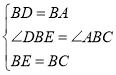 ,∴△BDE≌△BAC(SAS);
,∴△BDE≌△BAC(SAS);
(2)∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.
∵AD是正方形ABDI的對角線,∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC,∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,∴DE∥AG,∴四邊形ADEG是平行四邊形(一組對邊平行且相等).
(3)①當四邊形ADEG是矩形時,∠DAG=90°.
則∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°,即當∠BAC=135°時,平行四邊形ADEG是矩形;
②當四邊形ADEG是正方形時,∠DAG=90°,且AG=AD.
由①知,當∠DAG=90°時,∠BAC=135°.
∵四邊形ABDI是正方形,∴AD![]() AB.
AB.
又∵四邊形ACHG是正方形,∴AC=AG,∴AC![]() AB,∴當∠BAC=135°且AC
AB,∴當∠BAC=135°且AC![]() AB時,四邊形ADEG是正方形.
AB時,四邊形ADEG是正方形.


科目:初中數學 來源: 題型:
【題目】新定義:[a,b,c]為二次函數y=ax2+bx+e(a≠0,a,b,c為實數)的“圖象數”,如:y=-x2+2x+3的“圖象數”為[-1,2,3]
(1)二次函數y=![]() x2-x-1的“圖象數”為 .
x2-x-1的“圖象數”為 .
(2)若圖象數”是[m,m+1,m+1]的二次函數的圖象與x軸只有一個交點,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一張長方形紙片![]() (如圖①),
(如圖①),![]() ,將紙片折疊,使
,將紙片折疊,使![]() 落在
落在![]() 邊上,
邊上,![]() 為
為![]() 的對應點,折痕為
的對應點,折痕為![]() (如圖②),再將長方形
(如圖②),再將長方形![]() 以
以![]() 為折痕向右折疊,若點
為折痕向右折疊,若點![]() 落在
落在![]() 的三等分點上,則
的三等分點上,則![]() 的長為( )
的長為( )

A.8B.10C.8或10D.8或12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料:思考的同學小斌在解決連比等式問題:“已知正數![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的值”時,采用了引入參數法
的值”時,采用了引入參數法![]() ,將連比等式轉化為了三個等式,再利用等式的基本性質求出參數的值.進而得出
,將連比等式轉化為了三個等式,再利用等式的基本性質求出參數的值.進而得出![]() ,
,![]() ,
,![]() 之間的關系,從而解決問題.過程如下:
之間的關系,從而解決問題.過程如下:
解;設![]() ,則有:
,則有:
![]() ,
,![]() ,
,![]() ,
,
將以上三個等式相加,得![]() .
.
![]()
![]() ,
,![]() ,
,![]() 都為正數,
都為正數,
![]()
![]() ,即
,即![]() ,.
,.
![]()
![]() .
.
仔細閱讀上述材料,解決下面的問題:
(1)若正數![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,
,![]() ,
,![]() 互不相等,求證:
互不相等,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網絡中,△ABC的三個頂點都在格點上,點A、B、C的坐標分別為A(-2,4)、B(-2,0)、C(-4,1),結合所給的平面直角坐標系解答下列問題:
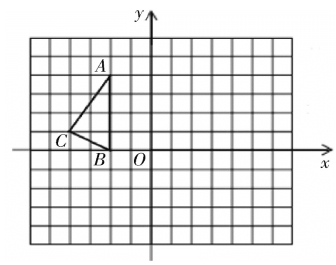
(1)畫出△ABC關于原點O中心對稱圖形△A1B1C1.
(2)平移△ABC,使點A移動到點A2(0,2),畫出平移后的△A2B2C2并寫出點B2、C2的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某市2018年企業用水量x(噸)與該月應交的水費y(元)之間的函數關系如圖.
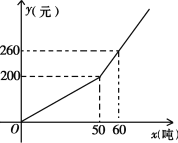
(1)當x≥50時,求y關于x的函數關系式;
(2)若某企業2018年10月份的水費為620元,求該企業2018年10月份的用水量.
查看答案和解析>>
科目:初中數學 來源: 題型:
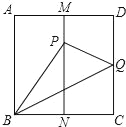
【題目】如圖,正方形ABCD中,AB=1,M,N分別是AD,BC邊的中點,沿BQ將△BCQ折疊,若點C恰好落在MN上的點P處,則PQ的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
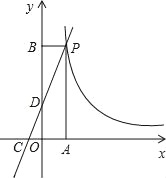
【題目】如圖,一次函數y=kx+2的圖象與反比例函數y=![]() 的圖象在第一象限的交點為P,PA⊥x軸于點A,PB⊥y軸于點B,函數y=kx+2的圖象分別交x軸,y軸于點C,D,已知△OCD的面積S△OCD=1,
的圖象在第一象限的交點為P,PA⊥x軸于點A,PB⊥y軸于點B,函數y=kx+2的圖象分別交x軸,y軸于點C,D,已知△OCD的面積S△OCD=1,![]() =
=![]()
(1)求點D的坐標;
(2)求k,m的值;
(3)寫出當x>0時,使一次函數y=kx+2的值大于反比例函數y=![]() 的值x的取值范圍.
的值x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年全球超級計算機500強名單公布,中國超級計算機“神威·太湖之光”和“天河二號”攜手奪得前兩名.已知“神威·太湖之光”的浮點運算速度是“天河二號”的2.74倍.這兩種超級計算機分別進行100億億次浮點運算,“神威·太湖之光”的運算時間比“天河二號”少18.75秒,求這兩種超級計算機的浮點運算速度.設“天河二號”的浮點運算速度為![]() 億億次/秒,依題意,可列方程為___________.
億億次/秒,依題意,可列方程為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com