【題目】元旦期間，小黃自駕游去了離家156千米的黃石礦博園，右圖是小黃離家的距離y（千米）與汽車行駛時間x（小時）之間的函數圖象．
（1）求小黃出發0.5小時時，離家的距離；
（2）求出AB段的圖象的函數解析式；
（3）小黃出發1.5小時時，離目的地還有多少千米？
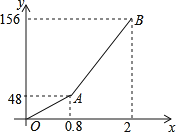
【答案】（1）30千米；（2）y＝90x﹣24（0.8≤x≤2）；（3）45千米
【解析】
（1）先運用待定系數法求出OA的解析式，再將x＝0.5代入，求出y的值即可；
（2）設AB段圖象的函數表達式為y＝k′x+b，將A、B兩點的坐標代入，運用待定系數法即可求解；
（3）先將x＝1.5代入AB段圖象的函數表達式，求出對應的y值，再用156減去y即可求解．
解：（1）設OA段圖象的函數表達式為y＝kx．
∵當x＝0.8時，y＝48，
∴0.8k＝48，
∴k＝60．
∴y＝60x（0≤x≤0.8），
∴當x＝0.5時，y＝60×0.5＝30．
故小黃出發0.5小時時，離家30千米；
（2）設AB段圖象的函數表達式為y＝k′x+b．
∵A（0.8，48），B（2，156）在AB上，
，
解得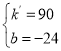
，
∴y＝90x﹣24（0.8≤x≤2）；
（3）∵當x＝1.5時，y＝90×1.5﹣24＝111，
∴156﹣111＝45．
故小黃出發1.5小時時，離目的地還有45千米．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，正六邊形ABCDEF的對稱中心P在反比例函數
的圖象上，邊CD在x軸上，點B在y軸上．已知
．
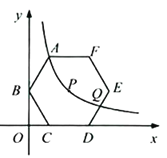
（1）點A是否在該反比例函數的圖象上？請說明理由．
（2）若該反比例函數圖象與DE交于點Q，求點Q的橫坐標．
（3）平移正六邊形ABCDEF，使其一邊的兩個端點恰好都落在該反比例函數的圖象上，試描述平移過程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“特色福州，美好生活”，福州舉行金色秋天旅游活動．明明和華華同學分析網上關于旅游活動的信息，發現最具特色的景點有：①鼓嶺、②森林公園、③青云山．他們準備周日下午去參觀游覽，各自在這三中個景點任選一個，每個景點被選中的可能性相同．
（1）明明同學在三個備選景點中選中鼓嶺的概率是 ．
（2）用樹狀圖或列表法求出明明和華華他們選中不同景點參觀的概率是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
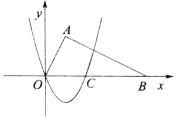
【題目】（2017貴州省遵義市）如圖，拋物線
（a＜0，a、b為常數）與x軸交于A、C兩點，與y軸交于B點，直線AB的函數關系式為
．
（1）求該拋物線的函數關系式與C點坐標；
（2）已知點M（m，0）是線段OA上的一個動點，過點M作x軸的垂線l分別與直線AB和拋物線交于D、E兩點，當m為何值時，△BDE恰好是以DE為底邊的等腰三角形？
（3）在（2）問條件下，當△BDE恰好是以DE為底邊的等腰三角形時，動點M相應位置記為點M′，將OM′繞原點O順時針旋轉得到ON（旋轉角在0°到90°之間）；
①探究：線段OB上是否存在定點P（P不與O、B重合），無論ON如何旋轉，
始終保持不變，若存在，試求出P點坐標；若不存在，請說明理由；
②試求出此旋轉過程中，（NA+
NB）的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】大學生小張利用暑假50天在一超市勤工儉學，被安排銷售一款成本為40元/件的新型商品，此類新型商品在第x天的銷售量p件與銷售的天數x的關系如下表：
x（天） | 1 | 2 | 3 | … | 50 |
p（件） | 118 | 116 | 114 | … | 20 |
銷售單價q（元/件）與x滿足：當1≤x＜25時q=x+60；當25≤x≤50時q=40+
．
（1）請分析表格中銷售量p與x的關系，求出銷售量p與x的函數關系．
（2）求該超市銷售該新商品第x天獲得的利潤y元關于x的函數關系式．
（3）這50天中，該超市第幾天獲得利潤最大？最大利潤為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為迎接：“國家衛生城市”復檢，某市環衛局準備購買A，B兩種型號的垃圾箱，通過市場調研得知：購買3個A型垃圾箱和2個B型垃圾箱共需540元，購買2個A型垃圾箱比購買3個B型垃圾箱少用160元．
（1）求每個A型垃圾箱和B型垃圾箱各多少元？
（2）該市現需要購買A，B兩種型號的垃圾箱共30個，其中買A型垃圾箱不超過16個．
①求購買垃圾箱的總花費w（元）與A型垃圾箱x（個）之間的函數關系式；
②當買A型垃圾箱多少個時總費用最少，最少費用是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
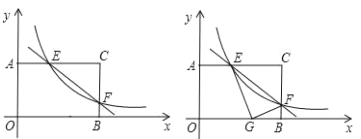
【題目】矩形AOBC中，OB＝4，OA＝3．分別以OB、OA所在直線為x軸、y軸，建立如圖1所示的平面直角坐標系．F是BC邊上一個動點（不與B、C重合）．過點F的反比例函數y＝
（k＞0）的圖象與邊AC交于點E．
（1）當點F運動到邊BC的中點時，點E的坐標為__________；
（2）連接EF，求∠EFC的正切值；
（3）如圖2，將△CEF沿EF折疊，點C恰好落在邊OB上的點G處，求BG的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點
，
，拋物線
交
軸正半軸于點
，連結
，
．
（1）求點的坐標；
（2）求直線的表達式；
（3）設拋物線分別交邊
，延長線于點
，
．
①若
，求拋物線表達式；
②若
與
相似，則
的值為 ．（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平行四邊形ABCD中，對角線AC，BD交于點O，E是邊AD上的一個動點(與點A，D不重合)，連接EO并延長，交BC于點F，連接BE，DF．下列說法:
① 對于任意的點E，四邊形BEDF都是平行四邊形;
② 當∠ABC>90°時，至少存在一個點E，使得四邊形BEDF是矩形;
③ 當AB<AD時，至少存在一個點E，使得是四邊形BEDF是菱形;
④ 當∠ADB=45°時，至少存在一個點E，使得是四邊形BEDF是正方形．
所有正確說法的序號是：_________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com