
【題目】如圖所示,若將類似于a、b、c、d四個圖的圖形稱做平面圖,則其頂點數、邊數與區域數之間存在某種關系.觀察圖b和表中對應的數值,探究計數的方法并作答.

(1)數一數每個圖中各有多少個頂點、多少條邊,這些邊圍出多少個區域并填表:
平面圖 | a | b | c | d |
頂點數(S) | 7 | |||
邊數(M) | 9 | |||
區域數(N) | 3 |
(2)根據表中數值,寫出平面圖的頂點數、邊數、區域數之間的一種關系為 ;
(3)如果一個平面圖有20個頂點和11個區域,那么利用(2)中得出的關系可知這個平面圖有 條邊.
【答案】(1)填表見解析;(2)S+N-M=1;(3)30.
【解析】試題分析:(1)按照自己熟悉的規律去數頂點數,邊數以及區域數;
(2)4+3-6=1,7+3-9=1,8+5-12=1,10+6-15=1,所以可得到一般規律:頂點數+區域數一邊數=1;
(3)邊數=頂點數+區域數-1.
試題解析:(1)數一數每個圖中各有多少個頂點、多少條邊,這些邊圍出多少個區域并填表:
平面圖 | a | b | c | d |
頂點數(S) | 4 | 7 | 8 | 10 |
邊數(M) | 6 | 9 | 12 | 15 |
區域數(N) | 3 | 3 | 5 | 6 |
(2)觀察表中數據可得;4+36=1,7+39=1,8+512=1,10+615=1
∴S+NM=1;(或頂點數+區域數一邊數=1)
故答案為:S+NM=1;
(3)由(2)得:邊數=頂點數+區域數1=20+111=30.
故答案為:30.


 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案科目:初中數學 來源: 題型:
【題目】對![]() ,
, ![]() 定義一種新運算
定義一種新運算![]() ,規定
,規定![]() (其中
(其中![]() ,
, ![]() 均為非零常數),這里等式右邊是通常的四則運算,例:
均為非零常數),這里等式右邊是通常的四則運算,例: ![]() .
.
已知![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)若關于m的不等式組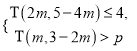 恰好有3個整數解,求實數
恰好有3個整數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=kx﹣4k+5的圖象與反比例函數y= ![]() (x>0)的圖象相交于點A(p,q).當一次函數y的值隨x的值增大而增大時,p的取值范圍是 .
(x>0)的圖象相交于點A(p,q).當一次函數y的值隨x的值增大而增大時,p的取值范圍是 . 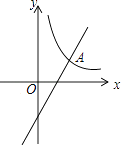
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅同學在做作業時,遇到這樣一道幾何題:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,過點E作EH⊥EF,垂足為E,交CD于H點.
(1)依據題意,補全圖形;
(2)求∠CEH的度數.
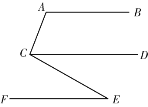
小明想了許久對于求∠CEH的度數沒有思路,就去請教好朋友小麗,小麗給了他如圖2所示的提示:

請問小麗的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中錯誤的是( )
A. 若∠C=∠A–∠B,則△ABC為直角三角形
B. 若a∶b∶c=2∶2∶2![]() ,則△ABC為直角三角形
,則△ABC為直角三角形
C. 若a=![]() c,b=
c,b=![]() c,則△ABC為直角三角形
c,則△ABC為直角三角形
D. 若∠A∶∠B∶∠C=3∶4∶5,則△ABC為直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場對一種新售的手機進行市場問卷調查,其中一個項目是讓每個人按A(不喜歡)、B(一般)、C(不比較喜歡)、D(非常喜歡)四個等級對該手機進行評價,圖①和圖②是該商場采集數據后,繪制的兩幅不完整的統計圖,請你根據以上統計圖提供的信息,回答下列問題:
(1)本次調查的人數為多少人?A等級的人數是多少?請在圖中補全條形統計圖.
(2)圖①中,a等于多少?D等級所占的圓心角為多少度?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△OAB的頂點A在x軸的正半軸上,頂點B的坐標為(3, ![]() ),點C的坐標為(
),點C的坐標為(![]() ,0),點P為斜邊OB上的一個動點,則PA+PC的最小值為( )
,0),點P為斜邊OB上的一個動點,則PA+PC的最小值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB=6,AD=10,∠BAD的平分線交BC于點E,交DC的延長線于點F,BG⊥AE,垂足為G,AG=2.5,則△CEF的周長為

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com