
【題目】定義![]() 為函數
為函數![]() 的特征數,下面給出特征數為
的特征數,下面給出特征數為![]() 的函數的一些結論:
的函數的一些結論:
①當![]() 時,函數圖象的頂點坐標是
時,函數圖象的頂點坐標是![]() ;
;
②當![]() 時,函數圖象截
時,函數圖象截![]() 軸所得的線段長度大于
軸所得的線段長度大于![]() ;
;
③當![]() 時,函數在
時,函數在![]() 時,
時,![]() 隨
隨![]() 的增大而減小;
的增大而減小;
④當![]() 時,函數圖象經過同一個點.
時,函數圖象經過同一個點.
其中正確的結論有( )
A. ①②③④ B. ①②④ C. ①③④ D. ②④
【答案】B
【解析】
①當m=-3時,根據函數式的對應值,可直接求頂點坐標;②當m>0時,直接求出圖象與x軸兩交點坐標,再求函數圖象截x軸所得的線段長度,進行判斷;③當m<0時,根據對稱軸公式,進行判斷;④當m≠0時,函數圖象經過同一個點.
根據定義可得函數y=2mx2+(1-m)x+(-1-m),
①當m=-3時,函數解析式為y=-6x2+4x+2,
∴![]() =
=![]() ,
,![]() ,
,
∴頂點坐標是(![]() ),正確;
),正確;
②函數y=2mx2+(1-m)x+(-1-m)與x軸兩交點坐標為(1,0),(-![]() ,0),
,0),
當m>0時,1-(-![]() )=
)=![]() >
>![]() ,正確;
,正確;
③當m<0時,函數y=2mx2+(1-m)x+(-1-m)開口向下,對稱軸x=![]() ,錯誤;
,錯誤;
④當m≠0時,x=1代入解析式y=0,則函數一定經過點(1,0),正確,
故選B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,M為AB中點.將△ACM沿CM翻折,得到△DCM(如圖2),P為CD上一點,再將△DMP沿MP翻折,使得D與B重合(如圖3),給出下列四個命題:
①BP∥AC;②△PBC≌△PMC;③PC⊥BM;④∠BPC=∠BMC.
其中真命題的個數是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求證:AD平分∠BAC;
(2)直接寫出AB+AC與AE之間的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊![]() ,點
,點![]() 為射線
為射線![]() 上一點,延長
上一點,延長![]() 至點
至點![]() ,使得
,使得![]() ,聯結
,聯結![]() 并延長交射線
并延長交射線![]() 于點
于點![]() 。
。
(1)當點![]() 在邊
在邊![]() 上時,如圖1,若
上時,如圖1,若![]() ,則
,則![]()
(2)當點![]() 在邊
在邊![]() 上時,如圖2,若
上時,如圖2,若![]() ,則(1)的結論還成立嗎?若成立,請證明;若不成立,寫出
,則(1)的結論還成立嗎?若成立,請證明;若不成立,寫出![]() 與
與![]() 的數量關系并證明。
的數量關系并證明。
(3)當點![]() 在邊
在邊![]() 的延長線上時,則(1)的結論還成立嗎?若成立,請證明;若不成立,寫出
的延長線上時,則(1)的結論還成立嗎?若成立,請證明;若不成立,寫出![]() 與
與![]() 的數量關系并證明。
的數量關系并證明。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象過點A(4,1)與正比例函數
的圖象過點A(4,1)與正比例函數![]() (
(![]() )的圖象相交于點B(
)的圖象相交于點B(![]() ,3),與
,3),與![]() 軸相交于點C.
軸相交于點C.
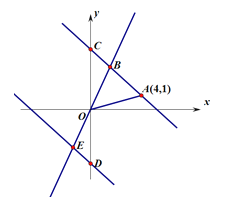
(1)求一次函數和正比例函數的表達式;
(2)若點D是點C關于![]() 軸的對稱點,且過點D的直線DE∥AC交BO于E,求點E的坐標;
軸的對稱點,且過點D的直線DE∥AC交BO于E,求點E的坐標;
(3)在坐標軸上是否存在一點![]() ,使
,使![]() .若存在請求出點
.若存在請求出點![]() 的坐標,若不存在請說明理由.
的坐標,若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,正方形的中心在原點![]() ,且正方形的一組對邊與
,且正方形的一組對邊與![]() 軸平行.點
軸平行.點![]() 是反比例幽數
是反比例幽數![]() 的圖象上與正方形的一個交點,若圖中陰影部分的面積等于
的圖象上與正方形的一個交點,若圖中陰影部分的面積等于![]() ,則
,則![]() 的值為( )
的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點
的圖象交于點![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.

![]() 求反比例函數
求反比例函數![]() 和一次函數
和一次函數![]() 的表達式;
的表達式;
![]() 連接
連接![]() ,
,![]() ,求
,求![]() 的面積;
的面積;
![]() 根據圖象寫出使一次函數的值小于反比例函數的值的
根據圖象寫出使一次函數的值小于反比例函數的值的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,則在下列條件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任選一個能判定△ABC≌△ABD的是( )
,則在下列條件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任選一個能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com