
【題目】如圖,在△ABC中,AC>AB,AD平分∠BAC,點D到點B與點C的距離相等,過點D作DE⊥BC于點E.
(1)求證:BE=CE;
(2)請直接寫出∠ABC,∠ACB,∠ADE三者之間的數(shù)量關(guān)系;
(3)若∠ACB=40°,∠ADE=20°,求∠DCB的度數(shù).
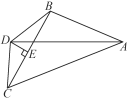
【答案】(1)見解析;(2)∠ABC-∠ACB=2∠ADE,理由見解析;(3)30°
【解析】
(1)利用等腰三角形底邊上三線合一即可證明.
(2)結(jié)論:∠ABC-∠ACB=2∠ADE.如圖2中,作BN⊥AD于N,交AC于M.證出∠ABN=∠AMN,再由角的和差求得。
(3)如圖3中,作DM⊥AC于M,DN⊥AB于N.首先證明△DBN≌△DCM,推出∠BDN=∠CDM,推出∠CDB=∠MDN,由∠CAB+∠MDN=180°,推出∠CDB+∠CAB=180°,
利用(2)的結(jié)論求出∠ABC,∠CAB即可解決問題.
(1)證明:如圖1中,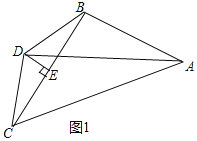
∵DB=DC,DE⊥BC,
∴CE=BE(等腰三角形底邊上三線合一).
(2)結(jié)論:∠ABC-∠ACB=2∠ADE.
理由:如圖2中,作BN⊥AD于N,交AC于M.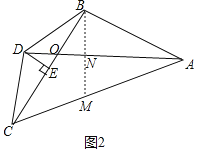
∵∠BAN=∠MAN,∠BAN+∠ABN=90°,∠MAN+∠AMN=90°,
∴∠ABN=∠AMN,
∵∠DOE=∠BON,∠DEO=∠BNO=90°,
∴∠EDA=∠CBM,
∴∠ABC-∠ACB=∠ABM+∠CBM-∠ACB=∠AMB+∠CBM-∠ABC=∠MCB+∠CBM+∠CBM-∠ACB=2∠CBN=2∠EDA.
故答案為∠ABC-∠ACB=2∠ADE
(3)解:如圖3中,作DM⊥AC于M,DN⊥AB于N.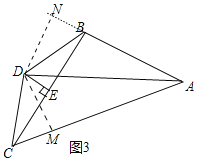
∵∠DAN=∠DAM,DM⊥AC,DN⊥AB,
∴DM=DN,
在Rt△DBN和Rt△DCM中,![]() ,
,
∴△DBN≌△DCM,
∴∠BDN=∠CDM,
∴∠CDB=∠MDN,
∵∠CAB+∠MDN=180°,
∴∠CDB+∠CAB=180°,
∵∠ACB=40°,∠ADE=20°,∠ABC-∠ACB=2∠ADE
∴∠ABC=80°,
∴∠CAB=180°-80°-40°=60°,
∴∠CDB=120°,
∴∠EDB=∠EDC=60°,
∴∠DCB=90°-∠EDC=30°.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】高速公路的同一側(cè)有A、B兩城鎮(zhèn),如圖,它們到高速公路所在直線MN的距離分別為AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之間建一個出口P,使A、B兩城鎮(zhèn)到P的距離之和最小.求這個最短距離.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)試說明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△ABC中,∠ABC=90°,AB=BC,三角形的頂點在相互平行的三條直線l1,l2,l3上,且l1,l2之間的距離為1,l2,l3之間的距離為2,則AC的長是( )

A. ![]() B.
B. ![]() C. 5 D.
C. 5 D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
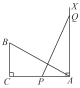
【題目】如圖,∠C=90°,AC=10,BC=5,AX⊥AC,點P和點Q從A點出發(fā),分別在線段AC和射線AX上運動,且AB=PQ,當(dāng)點P運動到AP=_______________時,△ABC與△QPA全等.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列運算正確的個數(shù)是( )
①2a2﹣a2=a2;
② ![]() +
+ ![]() =2
=2 ![]() ;
;
③(π﹣3.14)0× ![]() =0;
=0;
④a2÷a× ![]() =a2;
=a2;
⑤sin30°+cos60°= ![]() ;
;
⑥精確到萬位6295382≈6.30×106 .
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直角梯形AOCD的邊OC在x軸上,O為坐標(biāo)原點,CD垂直于x軸,D(5,4),AD=2.若動點E、F同時從點O出發(fā),E點沿折線OA→AD→DC運動,到達(dá)C點時停止;F點沿OC運動,到達(dá)C點時停止,它們運動的速度都是每秒1個單位長度.設(shè)E運動x秒時,△EOF的面積為y(平方單位),則y關(guān)于x的函數(shù)圖象大致為( )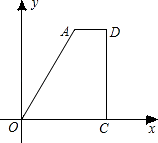
A.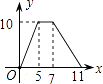
B.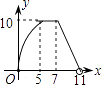
C.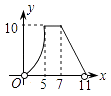
D.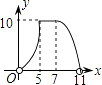
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D為BC邊的中點,過點D作DE⊥AB,DF⊥AC,垂足分別為E、F.
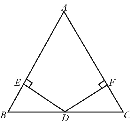
(1)求證;DE=DF;
(2)若∠A=90°,圖中與DE相等的還有哪些線段?(不用說明理由)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=﹣x2﹣2bx+c,當(dāng)x<2時,y的值隨x的增大而增大,則實數(shù)b的取值范圍是( )
A.b≥﹣1
B.b≤﹣1
C.b≥﹣2
D.b≤﹣2
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com