
科目:初中數學 來源: 題型:
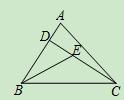
如圖,已知在△ABC中,CD是AB邊上的高線,BE平分∠ABC,交CD于點E,BC=5,DE=2,則△BCE的面積等于( )
A. 10 B. 7 C. 5 D. 4
B. 7 C. 5 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
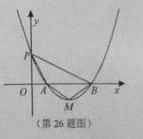
若關于x的二次函數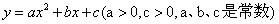 與x軸交于兩個不同的點
與x軸交于兩個不同的點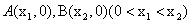 ,與y軸交于點P,其圖像頂點為點M,點O為坐標原點。
,與y軸交于點P,其圖像頂點為點M,點O為坐標原點。
(1)當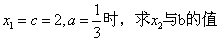 ;
;
(2)當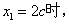 試問△ABM能否為等邊三角形?判斷并證明你的結論;
試問△ABM能否為等邊三角形?判斷并證明你的結論;
(3)當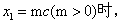 記△MAB,△PAB的面積分別為S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
記△MAB,△PAB的面積分別為S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
設二次函數y1=a(x−x1)(x−x2)(a≠0,x1≠x2)的圖象與一次函數y2=dx+e(d≠0)的圖象交于點(x1,0),若函數y=y2+y1的圖象與x軸僅有一個交點,則( )
)
A. a(x1−x2)=d B. a(x2−x1)=d C. a(x 1−x2)2=d D. a(x1+x2)2=d
1−x2)2=d D. a(x1+x2)2=d
查看答案和解析>>
科目:初中數學 來源: 題型:
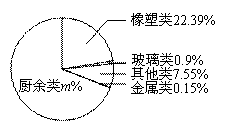
杭州市推行垃圾分類已經多年,但在廚余垃圾中除了廚余類垃圾還混雜著非廚余類垃 圾,如圖是杭州市某一天收到的廚余垃圾的統計圖
圾,如圖是杭州市某一天收到的廚余垃圾的統計圖
1) 試求出m的值
2) 杭州市那天共收到廚余垃圾約200噸,請計算其中混雜著的玻璃類垃圾的噸數
查看答案和解析>>
科目:初中數學 來源: 題型:
定義:長寬比為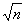 :1(n為正基數)的矩形稱為株為
:1(n為正基數)的矩形稱為株為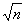 矩形. 下面,我們通過折疊的方式折出一個
矩形. 下面,我們通過折疊的方式折出一個 矩形.
矩形. 如圖①所示.
如圖①所示.
操作1:將正方形ABCD沿過點B的直線折疊,使折疊后的點C落在對角線BD上的點G處,折痕為BH
操作2:將AD沿過點G的直線折疊,使點A,點D分別落在邊AB,CD上,折痕為EF
則四 邊形BCEF為
邊形BCEF為 矩形
矩形
證明:設正方形ABCD的邊長為1,則BD=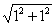 =
= .
.
由折疊性質可知BG=BC=1,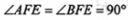 ,則四邊形BCEF為矩形
,則四邊形BCEF為矩形

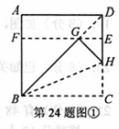
閱讀以上內容,回答下列問題:
(1) 在圖 中,所有與CH相等的線段是 ,tan
中,所有與CH相等的線段是 ,tan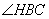 的值是
的值是
(2) 已知四邊形BCEF為 矩形,模仿上述操作,得到四邊形BCMN,如圖
矩形,模仿上述操作,得到四邊形BCMN,如圖 。
。
求證:四邊形BCMN是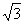 矩形
矩形
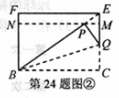
將圖 中的
中的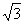 矩形BCM
矩形BCM N沿用(2)中的操作3次后,得到一個“
N沿用(2)中的操作3次后,得到一個“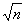 矩形”,則n的值是
矩形”,則n的值是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com