
【題目】小穎在二次函數y=2x2+4x+5的圖象上,依橫坐標找到三點(﹣1,y1),(2,y2),(﹣3,y3),則你認為y1 , y2 , y3的大小關系應為 .
 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(c≠4a),其圖象L經過點A(-2,0).
(1)求證:b2-4ac>0;
(2)若點B(-![]() ,b+3)在圖象L上,求b的值;
,b+3)在圖象L上,求b的值;
(3)在(2)的條件下,若圖象L的對稱軸為直線x=3,且經過點C(6,-8),點D(0,n)在y軸負半軸上,直線BD與OC相交于點E,當△ODE為等腰三角形時,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
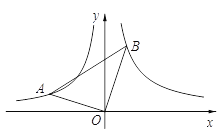
【題目】如圖,∠ AOB=90°,且點A,B分別在反比例函數![]() (x<0),
(x<0),![]() (x>0)的圖象上,且k1,k2分別是方程x2-x-6=0的兩根.
(x>0)的圖象上,且k1,k2分別是方程x2-x-6=0的兩根.
(1)求k1,k2的值;
(2)連接AB,求tan∠ OBA的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設拋物線C1:y=x2向右平移2個單位長度,再向下平移3個單位長度得到拋物線C2 , 則拋物線C2對應的函數解析式是( )
A.y=(x﹣2)2﹣3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x+2)2+3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A在數軸上對應的數為a,點B對應的數為b,且a、b滿足|a+3|+(b﹣2)2=0.
(1)求A、B兩點的對應的數a、b;
(2)點C在數軸上對應的數為x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求線段BC的長;
②在數軸上是否存在點P,使PA+PB=BC?求出點P對應的數;若不存在,說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將下列推證過程補充完整. 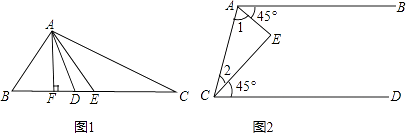
(1)如圖1,在△ABC中,AE是中線,AD是角平分線,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
(2)如圖2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() (點
(點![]() 與點
與點![]() 不重合),拋物線
不重合),拋物線![]() 經過點
經過點![]() ,拋物線的頂點為
,拋物線的頂點為![]() .
.
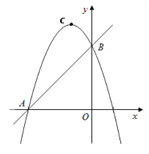
(1)![]() °;
°;
(2)求![]() 的值;
的值;
(3)在拋物線上是否存在點![]() ,能夠使
,能夠使![]() ?如果存在,請求出點
?如果存在,請求出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某蔬菜經營戶從蔬菜批發市場批發蔬菜進行零售,部分蔬菜批發價格與零售價格如表:
蔬菜品種 | 西紅柿 | 青椒 | 西蘭花 | 豆角 |
批發價(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售價(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
請解答下列問題:
(1)第一天,該經營戶批發西紅柿和西蘭花兩種蔬菜共300㎏,用去了1520元錢,這兩種蔬菜當天全部售完一共賺了多少元錢?
(2)第二天,該經營戶用1520元仍然批發西紅柿和西蘭花,要想當天全部售完后所賺錢數不少于1050元,則該經營戶最多能批發西紅柿多少㎏?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,對角線AC與BD相交于點E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四個結論:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.請寫出正確結論的序號(把你認為正確結論的序號都填上)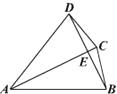
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com