
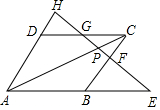
 如圖,過?ABCD的對角線AC上任一點P作一直線,分別交AB、BC、CD、DA所在直線于E、F、G、H.求證:PE•PF=PG•PH.
如圖,過?ABCD的對角線AC上任一點P作一直線,分別交AB、BC、CD、DA所在直線于E、F、G、H.求證:PE•PF=PG•PH. 分析 先利用平行四邊形的性質得到CD∥AB,AD∥BC,則利用相似三角形的判定得到△PCG∽△PAE,△PCF∽△PAH,根據相似三角形的性質得$\frac{PC}{PA}$=$\frac{PG}{PF}$,$\frac{PC}{PA}$=$\frac{PF}{PH}$,利用等量代換得到$\frac{PG}{PF}$=$\frac{PF}{PH}$,然后根據比例的性質即可得到結論.
解答 解:∵四邊形ABCD為平行四邊形,
∴CD∥AB,AD∥BC,
∵CG∥AE,
∴△PCG∽△PAE,
∴$\frac{PC}{PA}$=$\frac{PG}{PF}$,
∵CF∥AH,
∴△PCF∽△PAH,
∴$\frac{PC}{PA}$=$\frac{PF}{PH}$,
∴$\frac{PG}{PF}$=$\frac{PF}{PH}$,
∴PE•PF=PG•PH.
點評 本題考查了相似三角形的判定于性質:在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構造相似三角形;在利用相似三角形的性質時主要根據相似比表示線段之間的關系.


科目:初中數學 來源: 題型:填空題
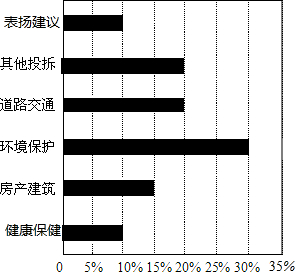 如圖是一家報紙“百姓熱線”一周內接到熱線電話的統計圖,其中有關環境保護問題的電話最多,共30個.本周“百姓熱線”共接到熱線電話有100個.
如圖是一家報紙“百姓熱線”一周內接到熱線電話的統計圖,其中有關環境保護問題的電話最多,共30個.本周“百姓熱線”共接到熱線電話有100個.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -$\frac{14}{3}$<a<-5 | B. | -5≤a<-$\frac{14}{3}$ | C. | -5<a≤-$\frac{14}{3}$ | D. | -$\frac{14}{3}$<a≤-5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com