
【題目】模型建立:如圖1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,過
,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() .
.
(1)求證:![]() ;
;
(2)模型應用:
①已知直線l1:![]() 與y軸交于
與y軸交于![]() 點,將直線l1繞著
點,將直線l1繞著![]() 點順時針旋轉45°至l2,如圖2,求l2的函數解析式;
點順時針旋轉45°至l2,如圖2,求l2的函數解析式;
②如圖3,長方形ABCO,![]() 為坐標原點,
為坐標原點,![]() 的坐標為(8,6),
的坐標為(8,6),![]() 、
、![]() 分別在坐標軸上,
分別在坐標軸上,![]() 是線段
是線段![]() 上動點,點
上動點,點![]() 是直線
是直線![]() 上的一點,若△APD是以點D為直角頂點的等腰Rt△,請直接寫出點
上的一點,若△APD是以點D為直角頂點的等腰Rt△,請直接寫出點![]() 的坐標.
的坐標.
【答案】(1)見解析;(2)①![]() ;②(-6,8)或(-2,0).
;②(-6,8)或(-2,0).
【解析】
(1)先根據△ABC為等腰直角三角形得出CB=CA,再由AAS定理可得△ACD≌△CBE,由全等三角形的性質可得![]() ;
;
(2)①如圖2中,設直線l1交x軸于B,作BP⊥AC于P,作PE⊥OB于E,PF⊥y軸于F.首先證明四邊形PEOF是正方形,求出點P的坐標,利用待定系數法即可解決問題.
②當點D為直角頂點,分點D在直線PA的上方或下方兩種情況,如圖3所示,當點D′在直線PA上方時,∠A D′P=90°時,A D′=P D′,設D′(x,-2x-4),利用三角形全等得到-2x-10=x+8,x=-6,OF=-2x-4 =8,即可得出結論;同理,再求出點D在直線PA下方時點![]() 的坐標.
的坐標.
(1)證明:如圖1中,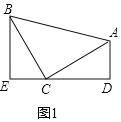
∵△ABC為等腰直角三角形,
∴BC=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD與△CBE中,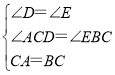 ,
,
∴△ACD≌△CBE(AAS);
∴![]() ;
;
(2)①如圖2中,設直線l1交x軸于B,作BP⊥AC于P,作PE⊥OB于E,PF⊥y軸于F.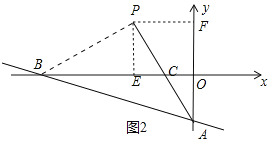
由(1)可知△PBE≌△PAF,
∴BE=AF,PE=PF,設PE=PF=a,
∵∠PEO=∠EOF=∠PFO=90°,
∴四邊形PEOF是矩形,
∵PE=PF,
∴四邊形PEOF是正方形,
∴OE=OF=a,
∵![]() =0時,x=-28,;x=0時,y=-4,
=0時,x=-28,;x=0時,y=-4,
∴B(-28,0),A(0,-4),
∴a+4+a=28,
∴a=12,
∴P(-12,12),設直線l2的解析式為y=kx+b則有![]() ,
,
解得 ,
,
∴直線l2的解析式為![]() ;
;
②如圖3中,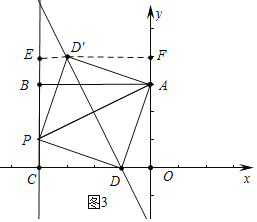
當點D位于直線![]() 上,點D為直角頂點時,分兩種情況,
上,點D為直角頂點時,分兩種情況,
當點D′在直線PA上方時,過D′作x軸的平行線EF,交直線OA于F,交直線BC于E,設D′(x,-2x-4);
則OF=-2x-4,AF=(-2x-4)-6=-2x-10,D′E=EF-D′F=x+8;
由(1)可知△AD′F≌△D′PE,得D′E=AF,即:
-2x-10=x+8,x=-6,OF=-2x-4 =8,
∴D′(-6,8);
當點D在直線PA下方時,同理可得D(-2,0),
綜上所述,滿足條件的點D的坐標為(-6,8)或(-2,0).


科目:初中數學 來源: 題型:
【題目】如圖:一把直尺壓住射線OB,另一把直尺壓住射線OA并且與第一把直尺交于點P,小明說:“射線OP就是∠BOA的角平分線.”他這樣做的依據是( )

A.角平分線上的點到這個角兩邊的距離相等
B.角的內部到角的兩邊的距離相等的點在角的平分線上
C.三角形三條角平分線的交點到三條邊的距離相等
D.以上均不正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,a,b,c分別是∠A、∠B、∠C的對邊
(1)若a=![]() ,c=4,求b
,c=4,求b
(2)若c=8,∠A=30°,求b
(3)若a:b=3:4,c=15,求Rt△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為菱形ABCD對角線的交點,M是射線CA上的一個動點(點M與點C、O、A都不重合),過點A、C分別向直線BM作垂線段,垂足分別為E、F,連接OE,OF.


(1)①依據題意補全圖形;
②猜想OE與OF的數量關系為_________________.
(2)小東通過觀察、實驗發現點M在射線CA上運動時,(1)中的猜想始終成立.
小東把這個發現與同學們進行交流,通過討論,形成了證明(1)中猜想的幾種想法:
想法1:由已知條件和菱形對角線互相平分,可以構造與△OAE全等的三角形,從而得到相等的線段,再依據直角三角形斜邊中線的性質,即可證明猜想;
想法2:由已知條件和菱形對角線互相垂直,能找到兩組共斜邊的直角三角形,例如其中的一組△OAB和△EAB,再依據直角三角形斜邊中線的性質,菱形四邊相等,可以構造一對以OE和OF為對應邊的全等三角形,即可證明猜想.
……
請你參考上面的想法,幫助小東證明(1)中的猜想(一種方法即可).
(3)當∠ADC=120°時,請直接寫出線段CF,AE,EF之間的數量關系是_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
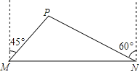
【題目】我市準備在相距![]() 千米的
千米的![]() ,
,![]() 兩工廠間修一條筆直的公路,但在
兩工廠間修一條筆直的公路,但在![]() 地北偏東
地北偏東![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 處,有一個半徑為
處,有一個半徑為![]() 千米的住宅小區(如圖),問修筑公路時,這個小區是否有居民需要搬遷?(參考數據:
千米的住宅小區(如圖),問修筑公路時,這個小區是否有居民需要搬遷?(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究:如圖①,在△ABC 中,∠BAC=90°,AB=AC,直線 m 經過點 A,BD⊥m 于點 D,CE⊥m 于點 E,求證:△ABD≌△CAE.
應用:如圖②,在△ABC 中,AB=AC,D、A、E 三點都在直線 m 上,并且有∠BDA=∠AEC=∠BAC,求證:DE=BD+CE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學研究課上,老師帶領大家探究《折紙中的數學問題》時,出示如圖1所示的長方形紙條![]() ,其中
,其中![]() ,
,![]() .然后在紙條上任意畫一條截線段
.然后在紙條上任意畫一條截線段![]() ,將紙片沿
,將紙片沿![]() 折疊,
折疊,![]() 與
與![]() 交于點
交于點![]() ,得到
,得到![]() .如圖2所示:
.如圖2所示:

探究:
(1)若![]() ,
,![]() ______°;
______°;
(2)改變折痕![]() 位置,
位置,![]() 始終是______三角形,請說明理由;
始終是______三角形,請說明理由;
應用:
(3)愛動腦筋的小明在研究![]() 的面積時,發現
的面積時,發現![]() 邊上的高始終是個不變的值.根據這一發現,他很快研究出
邊上的高始終是個不變的值.根據這一發現,他很快研究出![]() 的面積最小值為
的面積最小值為![]() ,此時
,此時![]() 的大小可以為______°;
的大小可以為______°;
(4)小明繼續動手操作,發現了![]() 面積的最大值.請你求出這個最大值.
面積的最大值.請你求出這個最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點C是⊙O上一點,連接BC,AC,過點C作直線CD⊥AB于點D,點E是AB上一點,直線CE交⊙O于點F,連接BF與直線CD延長線交于點G.求證:BC2=BG·BF.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com