已知直線l1∥l2，直線l3和直線l1、l2交于點C和D，在直線CD上有一點P．
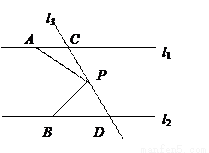
（1）如果P點在C、D之間運動時，問∠PAC，∠APB，∠PBD有怎樣的數量關系？請說明理由．
（2）若點P在C、D兩點的外側運動時（P點與點C、D不重合），試探索∠PAC，∠APB，∠PBD之間的關系又是如何？(請直接寫出答案，不需要證明)
文敬圖書課時先鋒系列答案科目：初中數學 來源： 題型：
如圖1所示，已知拋物線y=﹣x2+4x+5的頂點為D，與x軸交于A、B兩點，與y軸交于C點，E為對稱軸上的一點，連接CE，將線段CE繞點E按逆時針方向旋轉90°后，點C的對應點C′恰好落在y軸上．
（1）直接寫出D點和E點的坐標；
（2）點F為直線C′E與已知拋物線的一個交點，點H是拋物線上C與F之間的一個動點，若過點H作直線HG與y軸平行，且與直線C′E交于點G，設點H的橫坐標為m（0＜m＜4），那么當m為何值時，S△HGF：S△BGF=5：6？
（3）圖2所示的拋物線是由y=﹣x2+4x+5向右平移1個單位后得到的，點T（5，y）在拋物線上，點P是拋物線上O與T之間的任意一點，在線段OT上是否存在一點Q，使△PQT是等腰直角三角形？若存在，求出點Q的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
某校計劃開設4門選修課：音樂、繪畫、體育、舞蹈，學校采取隨機抽樣的方法進行問卷調查（每個被調查的學生必須選擇而且只能選擇其中一門），對調查結果進行統計后，繪制了如下不完整的兩個統計圖．
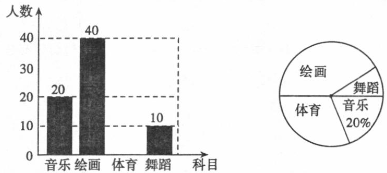
根據以上統計圖提供的信息，回答下列問題：
(1)此次調查抽取的學生人數為a=____人，其中選擇“繪畫”的學生人數占抽樣人數的百分比為b=____；
(2)補全條形統計圖，并求扇形統計圖中“舞蹈”所對應的圓心角的度數；
(3)若該校有2000名學生，請估計全校選擇“繪畫”的學生大約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
在平行四邊形ABCD中，點P從起點B出發，沿BC，CD逆時針方向向終點D勻速運動．設點P所走過的路程為x，則線段AP，AD與平行四邊形的邊所圍成的圖形面積為y，表示y與x的函數關系的圖象大致如下圖，則AB邊上的高是
 | |||
 | |||
A．3 B．4 C．5 D．6
查看答案和解析>>
科目：初中數學 來源： 題型：
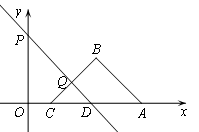
如圖，在平面直角
坐標系中，點 A(5,0)，B(3,2)，點C在線段OA上，BC=BA，點Q是線段BC上一個動點，點P的坐標是(0,3)，直線PQ的解析式為y=kx+b(k≠0)，且與x軸交于點D．
（1）求點C的坐標及b的值；
（2）求k的取值范圍；
（3）當k為取值范圍內的最大整數時，過點B作BE∥x軸，交PQ于點E，若拋物線y=ax2﹣5ax(a≠0)的頂點在四邊形ABED的內部，求a的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
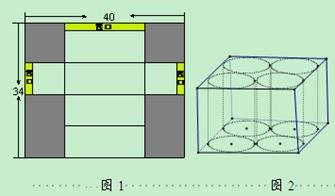
小葉爸爸開了一家茶葉專賣店．包裝設計專業畢業的小葉為他爸設計了一款用長方形厚紙片（厚度不計）做長方體茶葉包裝盒（如圖），陰影部分是裁剪掉的部分．沿圖中實線折疊做成的長方體紙盒的上下底面是正方形，有三處矩形形狀的“接口”用來折疊后粘貼或封蓋．
（1）若小葉用長40cm，寬34cm的矩形厚紙片，恰好能做成
一個符合要求的包裝盒，盒高是盒底邊長的2.5倍，三處“接口”的寬度相等．則該茶葉盒的容積是多少？
（2）小葉爸爸的茶葉專賣店以每盒150元購進一批茶葉，按進價增加20%作為售價，第一個月由于包裝粗糙，只售出不到一半但超過三分之一的量；第二個月采用了小葉的包裝后，馬上售完了余下的茶葉，但成本增加了每盒5元，售價仍不變．已知在整個買賣過程中共盈利1500元，求這批茶葉共進了多少盒？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
分
，若已知
和
，求
=__________
A．點A與點B B．點A與點D