
【題目】在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() 、
、![]() 的橫坐標(biāo)分別為
的橫坐標(biāo)分別為![]() 、
、![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖像經(jīng)過點(diǎn)
的圖像經(jīng)過點(diǎn)![]() 、
、![]() ,且
,且![]() 滿足
滿足![]() (
(![]() 為常數(shù)).
為常數(shù)).
(1)若一次函數(shù)![]() 的圖像經(jīng)過
的圖像經(jīng)過![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
①當(dāng)![]() 、
、![]() 時(shí),求
時(shí),求![]() 的值;
的值;
②若![]() 隨
隨![]() 的增大而減小,求
的增大而減小,求![]() 的取值范圍.
的取值范圍.
(2)當(dāng)![]() 且
且![]() 、
、![]() 時(shí),判斷直線
時(shí),判斷直線![]() 與
與![]() 軸的位置關(guān)系,并說明理由;
軸的位置關(guān)系,并說明理由;
(3)點(diǎn)![]() 、
、![]() 的位置隨著
的位置隨著![]() 的變化而變化,設(shè)點(diǎn)
的變化而變化,設(shè)點(diǎn)![]() 、
、![]() 運(yùn)動(dòng)的路線與
運(yùn)動(dòng)的路線與![]() 軸分別相交于點(diǎn)
軸分別相交于點(diǎn)![]() 、
、![]() ,線段
,線段![]() 的長(zhǎng)度會(huì)發(fā)生變化嗎?如果不變,求出
的長(zhǎng)度會(huì)發(fā)生變化嗎?如果不變,求出![]() 的長(zhǎng);如果變化,請(qǐng)說明理由.
的長(zhǎng);如果變化,請(qǐng)說明理由.
【答案】(1)k=-3,d>-4(3)不變
【解析】試題分析:(1)①由a,d的值,求得m的值,從而得到二次函數(shù)的表達(dá)式和A、B兩點(diǎn)的橫坐標(biāo),進(jìn)而得到A、B的坐標(biāo),即可得到![]() 的值.
的值.
②由![]() 、
、![]() 兩點(diǎn)在二次函數(shù)的圖像上,得到點(diǎn)
兩點(diǎn)在二次函數(shù)的圖像上,得到點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .再由在
.再由在![]() 中,
中, ![]() 隨
隨![]() 的增大而減小,
的增大而減小, ![]() ,得到
,得到![]() ,解不等式即可得到結(jié)論.
,解不等式即可得到結(jié)論.
(2)AB//x軸.當(dāng)d=-4時(shí),得到A、B兩點(diǎn)的縱坐標(biāo)相等且不為0,即可得到結(jié)論.
(3)當(dāng)點(diǎn)A運(yùn)動(dòng)到y軸上時(shí),a=0,得到點(diǎn)A的對(duì)應(yīng)點(diǎn)C的坐標(biāo)為(0,-2d),當(dāng)點(diǎn)B運(yùn)動(dòng)到y軸上時(shí),a=-2,得到點(diǎn)B的對(duì)應(yīng)點(diǎn)D的坐標(biāo)為(0,-2d-8),從而得到|CD|=8,故CD的長(zhǎng)不變.
試題解析:解:(1)①∵![]() ,∴
,∴![]() ,∴二次函數(shù)的表達(dá)式為
,∴二次函數(shù)的表達(dá)式為![]() .
.
∵![]() 、
、![]() 兩點(diǎn)的橫坐標(biāo)分別為
兩點(diǎn)的橫坐標(biāo)分別為![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() 、
、![]() 兩點(diǎn)的橫坐標(biāo)分別為
兩點(diǎn)的橫坐標(biāo)分別為![]() ,代入二次函數(shù)的表達(dá)式,得
,代入二次函數(shù)的表達(dá)式,得![]() 、
、![]() 兩點(diǎn)的縱坐標(biāo)分別為
兩點(diǎn)的縱坐標(biāo)分別為![]() ,即
,即![]() .
.
將點(diǎn)![]() 、
、![]() 的坐標(biāo)分別代入
的坐標(biāo)分別代入![]() ,得:
,得: ![]() ,解得:
,解得: ![]() ,∴
,∴![]() 的值為
的值為![]() .
.
②∵![]() ,∴
,∴![]() ,二次函數(shù)的表達(dá)式為
,二次函數(shù)的表達(dá)式為![]() .∵
.∵![]() 、
、![]() 兩點(diǎn)在二次函數(shù)的圖像上,∴點(diǎn)
兩點(diǎn)在二次函數(shù)的圖像上,∴點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .∵在
.∵在![]() 中,
中, ![]() 隨
隨![]() 的增大而減小,
的增大而減小, ![]() ,∴
,∴![]() ,解得:
,解得: ![]() .
.
(2)![]() 軸.理由如下:
軸.理由如下:
當(dāng)![]() 時(shí),
時(shí), ![]() .
.
∵![]() 、
、![]() ,∴
,∴![]() 、
、![]() 兩點(diǎn)的縱坐標(biāo)相等且不為0.又∵橫坐標(biāo)不等,∴
兩點(diǎn)的縱坐標(biāo)相等且不為0.又∵橫坐標(biāo)不等,∴![]() 軸.
軸.
(3)當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到
運(yùn)動(dòng)到![]() 軸上時(shí),
軸上時(shí), ![]() ,∴點(diǎn)
,∴點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)
的對(duì)應(yīng)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到
運(yùn)動(dòng)到![]() 軸上時(shí),
軸上時(shí), ![]() ,∴點(diǎn)
,∴點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)
的對(duì)應(yīng)點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,∴
,∴![]() ,∴
,∴![]() 的長(zhǎng)不變.
的長(zhǎng)不變.


 孟建平小學(xué)滾動(dòng)測(cè)試系列答案
孟建平小學(xué)滾動(dòng)測(cè)試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】菱形ABCD中,∠BAD=60°,BD是對(duì)角線,點(diǎn)E、F分別是邊AB、AD上兩個(gè)點(diǎn),且滿足AE=DF,連接BF與DE相交于點(diǎn)G.
(1)如圖1,求∠BGD的度數(shù);
(2)如圖2,作CH⊥BG于H點(diǎn),求證:2GH=GB+DG;
(3)在滿足(2)的條件下,且點(diǎn)H在菱形內(nèi)部,若GB=6,CH=4![]() ,求菱形ABCD的面積.
,求菱形ABCD的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】觀察下面三行單項(xiàng)式:
x,2x2,4x3,8x4,16x5,32x6,…;①
﹣2x,4x2,﹣8x3,16x4,﹣32x5,64x6,…;②
2x2,﹣3x3,5x4,﹣9x5,17x6,﹣33x7,…;③
根據(jù)你發(fā)現(xiàn)的規(guī)律,解答下列問題
(1)第①行的第8個(gè)單項(xiàng)式為 ;
(2)第②行的第9個(gè)單項(xiàng)式為 ;第③行的第10個(gè)單項(xiàng)式為 ;
(3)取每行的第9個(gè)單項(xiàng)式,令這三個(gè)單項(xiàng)式的和為A.當(dāng)x=![]() 時(shí),求512(A+
時(shí),求512(A+![]() )的值.
)的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
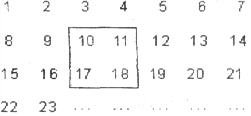
【題目】把正整數(shù)1,2,3,4,……,2009排列成如圖所示的一個(gè)表
(1)用一正方形在表中隨意框住4個(gè)數(shù),把其中最小的數(shù)記為x,另三個(gè)數(shù)用含x的式子表示出來,從小到大依次是 , , 。
(2)當(dāng)被框住的4個(gè)數(shù)之和等于416時(shí),x的值是多少?
(3)被框住的4個(gè)數(shù)之和能否等于622?如果能,請(qǐng)求出此時(shí)x的值;如果不能,請(qǐng)說明理由。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1已知矩形![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為矩形中心(
為矩形中心(![]() 與
與![]() 交點(diǎn)),現(xiàn)有兩動(dòng)點(diǎn)
交點(diǎn)),現(xiàn)有兩動(dòng)點(diǎn)![]() 分別沿著
分別沿著![]() 及
及![]() 的方向同時(shí)出發(fā)勻速運(yùn)動(dòng),速度都為每秒一個(gè)單位長(zhǎng)度,當(dāng)點(diǎn)
的方向同時(shí)出發(fā)勻速運(yùn)動(dòng),速度都為每秒一個(gè)單位長(zhǎng)度,當(dāng)點(diǎn)![]() 到達(dá)終點(diǎn)
到達(dá)終點(diǎn)![]() 時(shí)兩動(dòng)點(diǎn)都停止運(yùn)動(dòng),連接
時(shí)兩動(dòng)點(diǎn)都停止運(yùn)動(dòng),連接![]() ,在運(yùn)動(dòng)過程中,設(shè)運(yùn)動(dòng)時(shí)間為
,在運(yùn)動(dòng)過程中,設(shè)運(yùn)動(dòng)時(shí)間為![]() ,線段
,線段![]() 長(zhǎng)度為
長(zhǎng)度為![]() 個(gè)單位長(zhǎng)度,
個(gè)單位長(zhǎng)度,![]() 與
與![]() 的函數(shù)關(guān)系如圖2
的函數(shù)關(guān)系如圖2
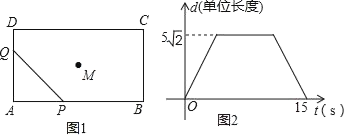
(1)![]()
![]() .
.
(2)![]() 為多少時(shí),線段
為多少時(shí),線段![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ?并且求出此時(shí)
?并且求出此時(shí)![]() 的度數(shù).
的度數(shù).
(3)運(yùn)動(dòng)過程中,連接![]() 和
和![]() ,求當(dāng)
,求當(dāng)![]() 為直角時(shí)的
為直角時(shí)的![]() 值.
值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
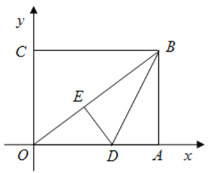
【題目】如圖,在平面直角坐標(biāo)系中,![]() 為坐標(biāo)原點(diǎn),矩形
為坐標(biāo)原點(diǎn),矩形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 、
、![]() ,將矩形
,將矩形![]() 的一個(gè)角沿直線
的一個(gè)角沿直線![]() 折疊,使得點(diǎn)
折疊,使得點(diǎn)![]() 落在對(duì)角線
落在對(duì)角線![]() 上的點(diǎn)
上的點(diǎn)![]() 處,折痕與
處,折痕與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(1)求線段![]() 的長(zhǎng)度;
的長(zhǎng)度;
(2)求直線![]() 所對(duì)應(yīng)的函數(shù)表達(dá)式;
所對(duì)應(yīng)的函數(shù)表達(dá)式;
(3)若點(diǎn)![]() 在線段
在線段![]() 上,在線段
上,在線段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使以
,使以![]() 為頂點(diǎn)的四邊形是平行四邊形?若存在,請(qǐng)求出點(diǎn)
為頂點(diǎn)的四邊形是平行四邊形?若存在,請(qǐng)求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】解方程:
(1)4(x﹣2)2﹣49=0.
(2)x2﹣5x﹣7=0.
(3)(2x+1)(x﹣2)=3.
(4)3x(x﹣2)=2(2﹣x).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解某地區(qū)30萬電視觀眾對(duì)新聞、動(dòng)畫、娛樂三類節(jié)目的喜愛情況,根據(jù)老年人、成年人、青少年各年齡段實(shí)際人口的比例3:5:2,隨機(jī)抽取一定數(shù)量的觀眾進(jìn)行調(diào)查,得到如下統(tǒng)計(jì)圖.
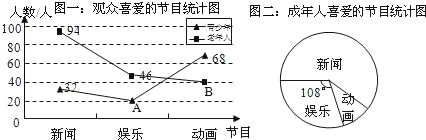
(1)上面所用的調(diào)查方法是 (填“全面調(diào)查”或“抽樣調(diào)查”);
(2)寫出折線統(tǒng)計(jì)圖中A、B所代表的值和抽取觀眾的總?cè)藬?shù)是多少;
(3)求該地區(qū)喜愛娛樂類節(jié)目的成年人的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
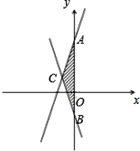
【題目】已知,直線 y=2x+3 與直線 y= ﹣ 2x ﹣ 1.
( 1 )求兩直線與 y 軸交點(diǎn)A,B的坐標(biāo);
( 2 )求兩直線交點(diǎn) C 的坐標(biāo);
( 3 )求 △ ABC 的面積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com