
【題目】已知二次函數(shù)![]() 圖象的頂點橫坐標是2,與
圖象的頂點橫坐標是2,與![]() 軸交于A(
軸交于A(![]() ,0)、B(
,0)、B(![]() ,0),
,0),![]() ﹤0﹤
﹤0﹤![]() ,與
,與![]() 軸交于點C,
軸交于點C,![]() 為坐標原點,
為坐標原點,![]() .
.
(1)求證:![]() ;
;
(2)求![]() 、
、![]() 的值;
的值;
(3)當![]() ﹥0且二次函數(shù)圖象與直線
﹥0且二次函數(shù)圖象與直線![]() 僅有一個交點時,求二次函數(shù)的最大值.
僅有一個交點時,求二次函數(shù)的最大值.
【答案】(1)證明見解析;(2) 當![]() 時,
時,![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
, ![]() ;(3)4.
;(3)4.
【解析】
試題分析:(1)因為圖象頂點的橫坐標是2,所以可證![]() ,從而證明結(jié)論成立;
,從而證明結(jié)論成立;
(2)根據(jù)拋物線頂點的橫坐標是2,可得![]() ,根據(jù)一元二次方程根與系數(shù)關(guān)系可得:
,根據(jù)一元二次方程根與系數(shù)關(guān)系可得:![]() ,
,![]() ,又因為tan∠CAO=
,又因為tan∠CAO=![]() ,tan∠CBO=
,tan∠CBO=![]() ,
,![]() ,可以求出
,可以求出![]() ,所以可得:
,所以可得:![]() ,然后分情況求出m、n的值;
,然后分情況求出m、n的值;
(3) 當![]() 時,可得二次函數(shù)的表達式為:
時,可得二次函數(shù)的表達式為:![]() ,根據(jù)二次函數(shù)圖象與直線
,根據(jù)二次函數(shù)圖象與直線![]() 僅有一個交點可得:一元二次方程
僅有一個交點可得:一元二次方程![]() 有兩個相等的實數(shù)根,從而得到:
有兩個相等的實數(shù)根,從而得到:![]() ,從而求出p的值,可以得到:此時二次函數(shù)的表達式為:
,從而求出p的值,可以得到:此時二次函數(shù)的表達式為:![]()
![]() ,從而得到函數(shù)的最大值是4.
,從而得到函數(shù)的最大值是4.
試題解析:(1)二次函數(shù)![]() 圖象頂點的橫坐標是
圖象頂點的橫坐標是![]() ,
,
將2代入頂點橫坐標得:![]()
∴![]() ,
,
(2) ∵已知二次函數(shù)圖象與![]() 軸交于A(
軸交于A(![]() ,0)、B(
,0)、B(![]() ,0),
,0),
由(1)知![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ﹤0﹤
﹤0﹤![]() ,
,
∴在Rt△ACO中,tan∠CAO=![]() ,
,
在Rt△CBO中,tan∠CBO=![]() ,
,
∵![]() ,
,
∴![]()
![]() ,
,
∵ ![]() ﹤0﹤
﹤0﹤![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]()
∴ ,
,
∴![]() ,
,
當![]() 時,
時,![]() ,
,
解得:![]() ,
,
當![]() 時,
時,![]() ,
,
解得:![]() ,
,
(3)當![]() 時,二次函數(shù)的表達式為:
時,二次函數(shù)的表達式為:![]() ,
,
∵二次函數(shù)圖象與直線![]() 僅有一個交點
僅有一個交點
∴方程組 僅有一個解
僅有一個解
∴一元二次方程![]()
即![]() 有兩個相等根,
有兩個相等根,
∴![]() ,
,
解得:![]() ,
,
此時二次函數(shù)的表達式為:![]()
![]() ,
,
∵![]() ,
,
∴![]() 有最大值
有最大值![]() .
.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC中,點A的坐標為(0,1),點C的坐標為(4,3),回答下列問題(直接寫出結(jié)果):
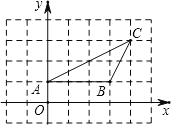
(1)點A關(guān)于原點對稱的點的坐標為
(2)點C關(guān)于y軸對稱的點的坐標為
(3)若△ABD與△ABC全等,則點D的坐標為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知一組數(shù)據(jù)x1,x2,x3,x4的平均數(shù)是5,則數(shù)據(jù)x1+3,x2+3,x3+3,x4+3的平均數(shù)是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
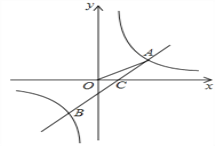
【題目】如圖,反比例函數(shù)y=![]() 與反比例函數(shù)y=k2
與反比例函數(shù)y=k2![]() +b的圖象的交點為A(m,1)、B(-2,n),OA與
+b的圖象的交點為A(m,1)、B(-2,n),OA與![]() 軸正方向的夾角為α,且tanα=
軸正方向的夾角為α,且tanα=![]() 。
。
(1)求反比例函數(shù)及一次函數(shù)的表達式;
(2)設(shè)直線AB與x軸交于點C,且AC與x軸正方向的夾角為β,求tanβ的值。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知圓O的直徑是方程x2﹣5x﹣24=0的根,且點A到圓心O的距離為6,則點A在( )
A.圓O上
B.圓O內(nèi)
C.圓O外
D.無法確定
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校八年級(二)班5位女生的體重(單位:kg)分別是:36,37,39,41,41.則這組數(shù)據(jù)的中位數(shù)是 .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com