
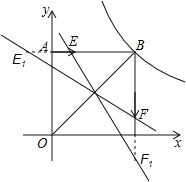
【題目】如圖,正方形AOCB在平面直角坐標(biāo)系xoy中,點O為原點,點B在反比例函數(shù)![]() (x>0)圖象上,△BOC的面積為8.
(x>0)圖象上,△BOC的面積為8.

(1)求反比例函數(shù)![]() 的關(guān)系
的關(guān)系
(2)若動點E從A開始沿AB向B以每秒1個單位的速度運動,同時動點F從B開始沿BC向C以每秒2個單位的速度運動,當(dāng)其中一個動點到達端點時,另一個動點隨之停止運動.若運動時間用t表示,△BEF的面積用S表示,求出S關(guān)于t的函數(shù)關(guān)系式?
(3)當(dāng)運動時間為![]() 秒時,在坐標(biāo)軸上是否存在點P,使△PEF的周長最小?若存在,請求出點P的坐標(biāo);若不存在,請說明理由.
秒時,在坐標(biāo)軸上是否存在點P,使△PEF的周長最小?若存在,請求出點P的坐標(biāo);若不存在,請說明理由.
【答案】(1)y=![]() ;(2)S=-
;(2)S=-![]() +4;(3)P(
+4;(3)P(![]() ,0)
,0)
【解析】
試題分析:(1)設(shè)點B的坐標(biāo)為(a,a),根據(jù)三角形的面積得出a的值,然后求出點B的坐標(biāo),計算反比例函數(shù)的解析式;(2)根據(jù)題意得出AE=t,BF=2t,BE=4-t,然后求出函數(shù)解析式;(3)根據(jù)對稱軸得出點P的坐標(biāo).
試題解析:(1)∵四邊形AOCB為正方形, ∴AB=BC=OC=OA,設(shè)點B坐標(biāo)為(a,a),∵![]() C=8,
C=8,
∴![]() =8, ∴a=±4 又∵點B在第一象限,∴點B坐標(biāo)為(4,4),
=8, ∴a=±4 又∵點B在第一象限,∴點B坐標(biāo)為(4,4),
將點B(4,4)代入y=![]() 得,k=16 ∴反比例函數(shù)解析式為y=
得,k=16 ∴反比例函數(shù)解析式為y=![]()
(2)∵運動時間為t,∴AE=t,BF=2t ∵AB=4,∴BE=4-t,
∴![]() =
=![]() (4-t)2t=-
(4-t)2t=-![]() +4t=--
+4t=--![]() +4,
+4,
(3)存在.
當(dāng)t=![]() 時,點E的坐標(biāo)為(
時,點E的坐標(biāo)為(![]() ,4),點F的坐標(biāo)為(4,
,4),點F的坐標(biāo)為(4,![]() )
)
作F點關(guān)于x軸的對稱點![]() ,得F1(4,-
,得F1(4,-![]() ),經(jīng)過點E、
),經(jīng)過點E、![]() 作直線
作直線
由E(![]() ,4),
,4),![]() (4,-
(4,-![]() )代入y=ax+b得:
)代入y=ax+b得: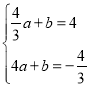 解得:
解得:
可得直線E![]() 的解析式是y=-2x+
的解析式是y=-2x+![]() 當(dāng)y=0時,x=
當(dāng)y=0時,x=![]() ∴P點的坐標(biāo)為(
∴P點的坐標(biāo)為(![]() ,0)
,0)


 導(dǎo)學(xué)教程高中新課標(biāo)系列答案
導(dǎo)學(xué)教程高中新課標(biāo)系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形![]() 中,
中,![]() ,
,![]() .分別以
.分別以![]() 所在直線為
所在直線為![]() 軸和
軸和![]() 軸,建立如圖所示的平面直角坐標(biāo)系.
軸,建立如圖所示的平面直角坐標(biāo)系.![]() 是邊
是邊![]() 上一點,過點
上一點,過點![]() 的反比例函數(shù)
的反比例函數(shù)![]() 圖象與
圖象與![]() 邊交于點
邊交于點![]() .
.
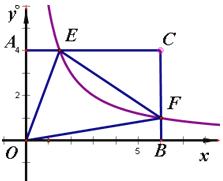
(1)請用k表示點E,F的坐標(biāo);
(2)若![]() 的面積為
的面積為![]() ,求反比例函數(shù)的解析式.
,求反比例函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c圖象上部分點的坐標(biāo)滿足下表:
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
則該函數(shù)圖象的頂點坐標(biāo)為___________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列運算結(jié)果正確的是( )
A.a4+a2=a6
B.(x-y)2=x2-y2
C.x6÷x2=x3
D.(ab)2=a2b2
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com