
【題目】如圖,拋物線y=(x﹣1)2+n與x軸交于A,B兩點(A在B的左側),與y軸交于點C(0,﹣3),點D與點C關于拋物線的對稱軸對稱.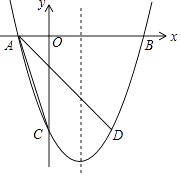
(1)求拋物線的解析式及點D的坐標;
(2)點P是拋物線對稱軸上的一動點,當△PAC的周長最小時,求出點P的坐標;
(3)點Q在x軸上,且∠ADQ=∠DAC,請直接寫出點Q的坐標.
【答案】
(1)
解:把C(0,﹣3)代入y=(x﹣1)2+n,得,﹣3=(0﹣1)2+n,
解得n=﹣4,
∴拋物線的解析式為y=(x﹣1)2﹣4,
∴拋物線的對稱軸為直線x=1,
∵點D與點C關于拋物線的對稱軸對稱,
∴點D的坐標為(2,﹣3)
(2)
解:連接PA、PC、PD
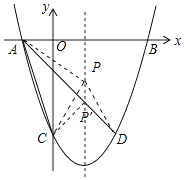
∵點D與點C關于拋物線的對稱軸對稱
∴PC=PD
∴AC+PA+PC=AC+PA+PD
∵AC為定值,PA+PD≥AD
∴當PA+PC的值最小,即A,P,D三點在同一直線上時△PAC的周長最小,
由y=(x﹣1)2﹣4=0解得,x1=﹣1,x2=3,
∵A在B的左側,∴A(﹣1,0),
由A,D兩點坐標可求得直線AD的解析式為y=﹣x﹣1,
當x=1時,y=﹣x﹣1=﹣2,
∴當△PAC的周長最小時,點P的坐標為(1,﹣2)
(3)
解:如圖2中,
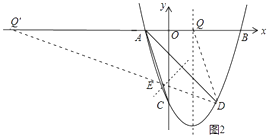
①作DQ∥AC交x軸于點Q,此時∠DQA=∠DAC,滿足條件.
∵A(﹣1,0),C(0,﹣3),
∴直線AC的解析式為y=﹣3x﹣3,
∴直線QD的解析式為y=﹣3x+3,
令y=0得x=1,
∴Q(1,0).
②設線段AD的垂直平分線交AC于E,直線DE與x的交點為Q′,此時∠Q′DA=′CAD,滿足條件,
∵直線AD的解析式為y=﹣x﹣1,
∴線段AD的中垂線是解析式為y=x﹣2,
由 ![]() 解得
解得  ,
,
∴E(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴直線DE的解析式為y=﹣ ![]() x﹣
x﹣ ![]() ,
,
令y=0得到x=﹣7,
∴Q′(﹣7,0).
綜上所述,Q點坐標為(1,0)或(﹣7,0)
【解析】(1)利用待定系數法即可求出n,利用對稱性C、D關于對稱軸對稱即可求出點D坐標.(2)A,P,D三點在同一直線上時△PAC的周長最小,求出直線AD的解析式即可解決問題.(3)分兩種情形①作DQ∥AC交x軸于點Q,此時∠DQA=∠DAC,滿足條件.②設線段AD的垂直平分線交AC于E,直線DE與x的交點為Q′,此時∠Q′DA=′CAD,滿足條件,分別求解即可.
【考點精析】根據題目的已知條件,利用二次函數的圖象和二次函數的性質的相關知識可以得到問題的答案,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:初中數學 來源: 題型:
【題目】如圖所示,AB、CD相交于點O,△AOC≌△BOD,點E、F分別在OA、OB上,要使△EOC≌△FOD,添加的一個條件不可能是( )

A. ∠OCE=∠ODF B. ∠CEA=∠DFB C. CE=DF D. OE=OF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,則下列結論:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB.其中正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,點D為△ABC內的一點,∠ADB=120°,∠ADC=90°,將△ABD繞點A逆時針旋轉60°得△ACE,連接DE. 
(1)求證:AD=DE;
(2)求∠DCE的度數;
(3)若BD=1,求AD,CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“足球運球”是中考體育必考項目之一.蘭州市某學校為了解今年九年級學生足球運球的掌握情況,隨機抽取部分九年級學生足球運球的測試成績作為一個樣本,按A,B,C,D四個等級進行統計,制成了如下不完整的統計圖.(說明:A級:8分﹣10分,B級:7分﹣7.9分,C級:6分﹣6.9分,D級:1分﹣5.9分)
根據所給信息,解答以下問題:
(1)在扇形統計圖中,C對應的扇形的圓心角是_____度;
(2)補全條形統計圖;
(3)所抽取學生的足球運球測試成績的中位數會落在_____等級;
(4)該校九年級有300名學生,請估計足球運球測試成績達到A級的學生有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把a、b兩個數中較小的數記作min{a,b},直線y=kx﹣k﹣2(k<0)與函數y=min{x2﹣1、﹣x+1}的圖象有且只有2個交點,則k的取值為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABM與△CDM是兩個全等的等邊三角形,MA⊥MD.有下列四個結論:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直線MB垂直平分線段CD;(4)四邊形ABCD是軸對稱圖形.其中正確結論的個數為( )
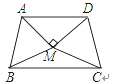
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)計算:
(1)3·(x4)6-2(x5·x3)3+x11·x13+x20·x3·x;
(2)(-4×103)2×(-2×103)2;
(3) ![]() 100×
100×![]() 99×
99×![]() 100;
100;
(4) ![]() 2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
(5)162m÷42n÷4m×43m-3n+1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《中華人民共和國道路交通管理條例》規定:小汽車在城街路上行駛速度不得超過70 km/h,如圖,一輛小汽車在一條城市街路上直道行駛,某一時刻剛好行駛到路面車速檢測儀 A的正前方60 m處的C點,過了5 s后,測得小汽車所在的B點與車速檢測儀A之間的距離為100 m.
(1)求B,C間的距離.
(2)這輛小汽車超速了嗎?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com