
【題目】某乒乓球館普通票價20元/張,暑假為了促銷,新推出兩種優惠卡:①金卡售價600元/張,每次憑卡不再收費;②銀卡售價150元/張,每次憑卡另收10元;暑期普通票正常出售,兩種優惠卡僅限暑期使用,不限次數.設打乒乓x次時,所需總費用為y元.
(1)分別寫出選擇銀卡、普通票消費時,y與x之間的函數關系式;
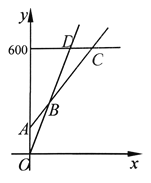
(2)在同一個坐標系中,若三種消費方式對應的函數圖像如圖所示,請根據函數圖像,寫出選擇哪種消費方式更合算.
【答案】(1)![]() ,
,![]() ;(2)當打球次數不足15次時,選擇普通票最合算,當打球次數介于15次到45次之間時,選擇銀卡最合算,當打球次數超過45次時,選擇金卡最合算,當打球次數恰為15次時,選擇普通票或銀卡同為最合算,當打球次數恰為45次時,選擇金卡或銀卡同為最合算.
;(2)當打球次數不足15次時,選擇普通票最合算,當打球次數介于15次到45次之間時,選擇銀卡最合算,當打球次數超過45次時,選擇金卡最合算,當打球次數恰為15次時,選擇普通票或銀卡同為最合算,當打球次數恰為45次時,選擇金卡或銀卡同為最合算.
【解析】
(1)根據銀卡售價150元/張,每次憑卡另收10元,以及旅游館普通票價20元/張,設游泳x次時,分別得出所需總費用為y元與x的關系式即可;
(2)利用函數交點坐標求法分別得出即可,利用點的坐標以及結合得出函數圖象得出答案.
解:(1)選擇銀卡消費時,y與x之間的函數關系式為:![]()
選擇普通票消費時,y與x之間的函數關系式為:![]()
(2)根據題意,分別求出A(0,150)、B(15,300)、C(45,600)
∴當打球次數不足15次時,選擇普通票最合算,當打球次數介于15次到45次之間時,選擇銀卡最合算,當打球次數超過45次時,選擇金卡最合算,當打球次數恰為15次時,選擇普通票或銀卡同為最合算,當打球次數恰為45次時,選擇金卡或銀卡同為最合算.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90,AC=BC=1,E、F為線段AB上兩動點,且∠ECF=45°,過點E、F分別作BC、AC的垂線相交于點M,垂足分別為H、G.現有以下結論:①AB=![]() ;②當點E與點B重合時,MH=
;②當點E與點B重合時,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正確結論為( )
,其中正確結論為( )
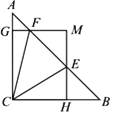
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD,AD=![]() ,將矩形ABCD繞著頂點B順時針旋轉,得到矩形EBGF,頂點A、D、C分別與點E、F、G對應(點D與點F不重合).如果點D、E、F在同一條直線上,那么線段DF的長是____.(用含
,將矩形ABCD繞著頂點B順時針旋轉,得到矩形EBGF,頂點A、D、C分別與點E、F、G對應(點D與點F不重合).如果點D、E、F在同一條直線上,那么線段DF的長是____.(用含![]() 的代數式表示)
的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某底面為圓形的古塔剖面和山坡的剖面在同一平面上,古塔EF(F為塔底的中心)與地面BD垂直,古塔的底面直徑CD=8米,BC=10米,斜坡AB=26米,斜坡坡面AB的坡度i=5:12,在坡腳的點A處測得古塔頂端點E的仰角∠GAE=47°,則古塔EF的高度約( )(參考數據:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
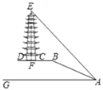
A. 27.74米B. 30.66米C. 35.51米D. 40.66米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,△ABC為等邊三角形,點D為直線BC上一動點(點D不與B、C重合).以
AD為邊作菱形ADEF,使∠DAF=60°,連接CF.
⑴如圖1,當點D在邊BC上時,
求證:∠ADB=∠AFC;②請直接判斷結論∠AFC=∠ACB+∠DAC是否成立;
⑵如圖2,當點D在邊BC的延長線上時,其他條件不變,結論∠AFC=∠ACB+∠DAC是否成立?請寫出∠AFC、∠ACB、∠DAC之間存在的數量關系,并寫出證明過程;
⑶如圖3,當點D在邊CB的延長線上時,且點A、F分別在直線BC的異側,其他條件不變,請補全圖形,并直接寫出∠AFC、∠ACB、∠DAC之間存在的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 的坐標為
的坐標為![]() ,動點
,動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 軸以每秒
軸以每秒![]() 個單位的速度向上移動,且過點
個單位的速度向上移動,且過點![]() 的直線
的直線![]() 也隨之移動,如果點
也隨之移動,如果點![]() 關于
關于![]() 的對稱點落在坐標軸上,沒點
的對稱點落在坐標軸上,沒點![]() 的移動時間為
的移動時間為![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.

查看答案和解析>>
科目:初中數學 來源: 題型:
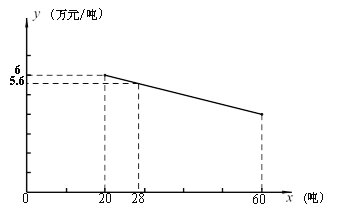
【題目】某工廠生產一種產品,當生產數量至少為20噸,但不超過60噸時,每噸的成本![]() (萬元/噸)與生產數量
(萬元/噸)與生產數量![]() (噸)之間是一次函數關系,其圖像如圖所示.
(噸)之間是一次函數關系,其圖像如圖所示.
(1)求出![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(2)如果每噸的成本是4.8萬元,求該產品的生產數量;
(3)當生產這種產品的總成本是200萬元時,求該產品的生產數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
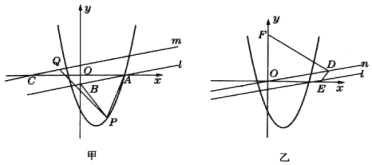
【題目】如圖所示,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于
軸交于![]() 點,經過點
點,經過點![]() 的拋物線
的拋物線![]() 上有一動點
上有一動點![]() ,且點
,且點![]() 在直線
在直線![]() 的下方.
的下方.
(1)平移直線![]() 經過點
經過點![]() ,得到直線
,得到直線![]() ,點
,點![]() 為直線
為直線![]() 上一個動點,連接
上一個動點,連接![]() ,當
,當![]() 面積最大時,求
面積最大時,求![]() 的最小值.
的最小值.
(2)平移直線![]() 經過原點,得到直線
經過原點,得到直線![]() ,點
,點![]() 是直線
是直線![]() 上一點,且
上一點,且![]() 點橫坐標為6,點
點橫坐標為6,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,當
軸上,當![]() 時,拋物線上是否存在點
時,拋物線上是否存在點![]() ,使四邊形
,使四邊形![]() 是矩形?如果存在,請求出點
是矩形?如果存在,請求出點![]() 的坐標,如果不存在,請說明理由.
的坐標,如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線EF與⊙O相切于點C,點A為⊙O上異于點C的一動點,⊙O的半徑為4,AB![]() EF于點B,設
EF于點B,設![]() ACF=α(0°<α<180°).
ACF=α(0°<α<180°).
(1)若α=![]() ,求證:四邊形OCBA為正方形;
,求證:四邊形OCBA為正方形;
(2)若AC―AB=1,求AC的長;
(3)當AC―AB取最大值時,求α的度數.
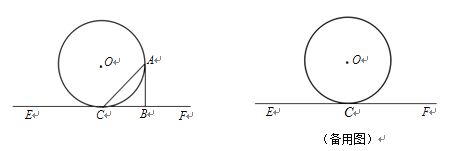
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com