
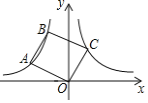
【題目】如圖,點(diǎn)A、B在雙曲線![]() (x<0)上,連接OA、AB,以OA、AB為邊作OABC.若點(diǎn)C恰落在雙曲線
(x<0)上,連接OA、AB,以OA、AB為邊作OABC.若點(diǎn)C恰落在雙曲線![]() (x>0)上,此時(shí)OABC的面積為( ).
(x>0)上,此時(shí)OABC的面積為( ).
A.![]() B.
B.![]() C.
C.![]() D.4
D.4![]()
【答案】B
【解析】
連接AC,過A作AD⊥x軸于D,過C作CE⊥x軸于E,過B作BF⊥AD于F,利用AAS證出△ABF≌△COE,設(shè)A(a,﹣![]() ),C(b,
),C(b,![]() ),則OE=BF=b,CE=AF=
),則OE=BF=b,CE=AF=![]() ,即可表示出點(diǎn)B的坐標(biāo),然后代入反比例函數(shù)的解析式中即可求出
,即可表示出點(diǎn)B的坐標(biāo),然后代入反比例函數(shù)的解析式中即可求出![]() ,然后根據(jù)平行四邊形OABC的面積=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出結(jié)論.
,然后根據(jù)平行四邊形OABC的面積=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可求出結(jié)論.
解:如圖,連接AC,過A作AD⊥x軸于D,過C作CE⊥x軸于E,過B作BF⊥AD于F,

∵FD⊥x軸,CE⊥x軸
∴FD∥CE
∴∠FAC=∠ECA
∵四邊形AOCB是平行四邊形
∴BA∥OC,BA=OC,∠BAC=∠OCA
∴∠FAB=∠FAC-∠BAC=∠ECA-∠OCA=∠ECO
在△ABF和△COE中
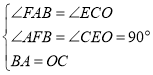
∴△ABF≌△COE,
設(shè)A(a,﹣![]() ),C(b,
),C(b,![]() ),則OE=BF=b,CE=AF=
),則OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
又∵點(diǎn)B在雙曲線y=-![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
∴![]() ﹣
﹣![]() =2,
=2,
設(shè)![]() =x,則方程
=x,則方程![]() ﹣
﹣![]() =2可化為3x﹣
=2可化為3x﹣![]() =2,
=2,
解得x=![]() 或x=
或x=![]() (a和b異號(hào),故舍去),
(a和b異號(hào),故舍去),
∴![]() =
=![]() ,
,
∴![]() =﹣
=﹣![]() ,
,
∴平行四邊形OABC的面積=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×|﹣3|﹣
×|﹣3|﹣![]() ×|2|]
×|2|]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=﹣3×![]() ﹣2×(﹣
﹣2×(﹣![]() )
)
=2![]() .
.
故選B.


 名題金卷系列答案
名題金卷系列答案 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】仙桃是遂寧市某地的特色時(shí)令水果.仙桃一上市,水果店的老板用2400元購進(jìn)一批仙桃,很快售完;老板又用3700元購進(jìn)第二批仙桃,所購件數(shù)是第一批的![]() 倍,但進(jìn)價(jià)比第一批每件多了5元.
倍,但進(jìn)價(jià)比第一批每件多了5元.
(1)第一批仙桃每件進(jìn)價(jià)是多少元?
(2)老板以每件225元的價(jià)格銷售第二批仙桃,售出80%后,為了盡快售完,剩下的決定打折促銷.要使得第二批仙桃的銷售利潤(rùn)不少于440元,剩余的仙桃每件售價(jià)至少打幾折?(利潤(rùn)=售價(jià)﹣進(jìn)價(jià))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)在一節(jié)數(shù)學(xué)探究課上,學(xué)生們發(fā)現(xiàn)了一個(gè)規(guī)律:
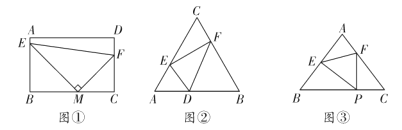
如圖①,當(dāng)四邊形![]() 是矩形時(shí),
是矩形時(shí),![]() 的直角頂點(diǎn)M在
的直角頂點(diǎn)M在![]() 邊上運(yùn)動(dòng),直角邊分別與線段
邊上運(yùn)動(dòng),直角邊分別與線段![]() 、線段
、線段![]() 交于E、F兩點(diǎn),在點(diǎn)M運(yùn)動(dòng)的過程中,始終存在著
交于E、F兩點(diǎn),在點(diǎn)M運(yùn)動(dòng)的過程中,始終存在著![]() .于是又有同學(xué)提出了問題,如果將四邊形換成三角形時(shí),是否仍存在同樣的規(guī)律呢?如圖②,在
.于是又有同學(xué)提出了問題,如果將四邊形換成三角形時(shí),是否仍存在同樣的規(guī)律呢?如圖②,在![]() 中,
中,![]() ,點(diǎn)D為
,點(diǎn)D為![]() 邊上的動(dòng)點(diǎn),過點(diǎn)D作
邊上的動(dòng)點(diǎn),過點(diǎn)D作![]() ,交
,交![]() 于點(diǎn)E,交
于點(diǎn)E,交![]() 于點(diǎn)F,請(qǐng)問是否存在兩個(gè)相似的三角形,若存在,請(qǐng)證明;若不存在,請(qǐng)說明理由;
于點(diǎn)F,請(qǐng)問是否存在兩個(gè)相似的三角形,若存在,請(qǐng)證明;若不存在,請(qǐng)說明理由;
(2)結(jié)合上述規(guī)律,解決下列問題:
如圖③,在![]() 中,
中,![]() ,
,![]() ,點(diǎn)P為
,點(diǎn)P為![]() 上一點(diǎn)(不與B、C重合),過點(diǎn)P作
上一點(diǎn)(不與B、C重合),過點(diǎn)P作![]() 于點(diǎn)E,
于點(diǎn)E,![]() 交
交![]() 于點(diǎn)F,若
于點(diǎn)F,若![]() 為等腰三角形,求
為等腰三角形,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1是一個(gè)由1~28的連續(xù)整數(shù)排成的“數(shù)陣”.如圖2,用2×2的方框圍住了其中的四個(gè)數(shù),如果圍住的這四個(gè)數(shù)中的某三個(gè)數(shù)的和是27,那么這三個(gè)數(shù)是a,b,c,d中的_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
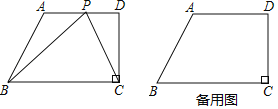
【題目】如圖所示,在四邊形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,且AD=12,BC=18.動(dòng)點(diǎn)P從點(diǎn)A出發(fā),以每秒2個(gè)單位長(zhǎng)度的速度向點(diǎn)D運(yùn)動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t秒(0<t≤6)
(1)當(dāng)t=6時(shí),cos∠BPC= ;
(2)當(dāng)△BPC的外接圓與AD相切時(shí),求t的值;
(3)在點(diǎn)P運(yùn)動(dòng)過程中,cos∠BPC是否存在最小值?若存在,請(qǐng)求出這個(gè)最小值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在銳角三角形ABC中,點(diǎn)D,E分別在邊AC,AB上,AG⊥BC于點(diǎn)G,AF⊥DE于點(diǎn)F,∠EAF=∠GAC.
(1)求證:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
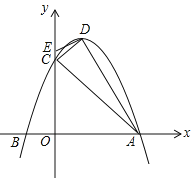
【題目】已知,拋物線![]() (a<0)與x軸交于A(3,0)、B兩點(diǎn),與y軸交于點(diǎn)C,拋物線的對(duì)稱軸是直線x=1,D為拋物線的頂點(diǎn),點(diǎn)E在y軸C點(diǎn)的上方,且CE=
(a<0)與x軸交于A(3,0)、B兩點(diǎn),與y軸交于點(diǎn)C,拋物線的對(duì)稱軸是直線x=1,D為拋物線的頂點(diǎn),點(diǎn)E在y軸C點(diǎn)的上方,且CE=![]() .
.
(1)求拋物線的解析式及頂點(diǎn)D的坐標(biāo);
(2)求證:直線DE是△ACD外接圓的切線;
(3)在直線AC上方的拋物線上找一點(diǎn)P,使![]() ,求點(diǎn)P的坐標(biāo);
,求點(diǎn)P的坐標(biāo);
(4)在坐標(biāo)軸上找一點(diǎn)M,使以點(diǎn)B、C、M為頂點(diǎn)的三角形與△ACD相似,直接寫出點(diǎn)M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)y=﹣x2+bx﹣c,它與x軸交于A、B,且A、B位于原點(diǎn)兩側(cè),與y的正半軸交于C,頂點(diǎn)D在y軸右側(cè)的直線l:y=4上,則下列說法:①bc<0;②0<b<4;③AB=4;④S△ABD=8.其中正確的結(jié)論有( )
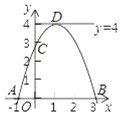
A.①②B.②③C.①②③D.①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,過點(diǎn)A(0,4)的圓的圓心坐標(biāo)為C(2,0),B是第一象限圓弧上的一點(diǎn),且BC⊥AC,拋物線![]() 經(jīng)過C、B兩點(diǎn),與x軸的另一交點(diǎn)為D.
經(jīng)過C、B兩點(diǎn),與x軸的另一交點(diǎn)為D.
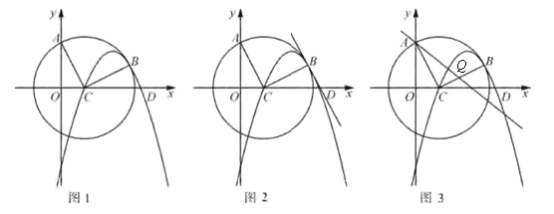
(1)點(diǎn)B的坐標(biāo)為( , ),拋物線的表達(dá)式為 .
(2)如圖2,求證:BD//AC;
(3)如圖3,點(diǎn)Q為線段BC上一點(diǎn),且AQ=5,直線AQ交⊙C于點(diǎn)P,求AP的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com