
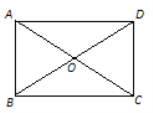
【題目】如圖,在矩形ABCD中,對角線AC、BD相交于O,且AC=2AB.
(1)你能說明△AOB是等邊三角形嗎?請寫出理由;
(2)若AB=1,求點D到AC的距離.
【答案】(1)△OAB是等邊三角形(2)DE=![]()
【解析】試題分析:(1)根據矩形的對角線互相平分且相等可得OA=OB,再求出AB=![]() AC,然后根據三條邊都相等的三角形是等邊三角形解答;
AC,然后根據三條邊都相等的三角形是等邊三角形解答;
(2)在Rt△ABC中,根據勾股定理求出BC的長, 作DE⊥AC于E,利用三角形的面積法即可求得DE長.
試題解析:(1)△OAB是等邊三角形, 理由如下:
在矩形ABCD中,OA=OC,OB=OD, AC=BD,
∴ OA=![]() AC,OB=
AC,OB=![]() BD.
BD.
又∵ AB=![]() AC,
AC,
∴ OA=OB=AB,
即△OAB是等邊三角形;
(2)在Rt△ABC中,AB=1,AC=2,
根據勾股定理,得BC=![]() ,
,
作DE⊥AC于E,
∴ DE·AC=AD·DC,
∴ DE=![]()



科目:初中數學 來源: 題型:
【題目】如圖,已知AB ![]() ,在AB,CD之間取一點E,連接EA,EC,試探索
,在AB,CD之間取一點E,連接EA,EC,試探索![]() AEC與
AEC與![]() EAB,
EAB,![]() ECD之間的關系
ECD之間的關系![]() 若點E取在AC上
若點E取在AC上![]() 如圖
如圖![]() ,則
,則![]() AEC
AEC![]() ,由此可得
,由此可得![]() AEC
AEC![]() EAB
EAB![]() ECD或
ECD或![]() AEC
AEC![]() EAB
EAB![]() ECD
ECD![]() 如果點E取在AC的兩側
如果點E取在AC的兩側![]() 如圖
如圖![]() ,結論會是什么?
,結論會是什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 為⊙
為⊙![]() 上一點,點
上一點,點![]() 在直徑
在直徑![]() 的延長線上,且
的延長線上,且![]() .
.
(1)判斷直線![]() 和⊙
和⊙![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
(2)過點![]() 作⊙
作⊙![]() 的切線
的切線![]() 交直線
交直線![]() 于點
于點![]() ,若
,若![]() ,⊙
,⊙![]() 的半徑是
的半徑是![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A.正數和負數統稱為有理數
B.0是最小的有理數
C.如果兩個數的絕對值相等,那么這兩個數一定相等
D.互為相反數的兩個數之和為零
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下列推理說明:如圖,已知AB∥DE,且有∠1=∠2,∠3=∠4,
∵AB∥DE( )
∴∠1= (根據兩直線平行,同位角相等)
∵∠1= , ∠3=∠4(已知)
∴∠2= (等量代換)
∴BC∥EF(根據___________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鎮正在建造的文化廣場工地上,有兩種鋪設廣場地面的材料,一種是長為![]() cm,寬為
cm,寬為![]() cm的長方形板材(如圖),另一種是邊長為
cm的長方形板材(如圖),另一種是邊長為![]() cm的正方形地磚(如圖②)
cm的正方形地磚(如圖②)

(1)用幾塊如圖②所示的正方形地磚能拼出一個新的正方形?并寫出新正方形的面積
(寫出一個符合條件的答案即可);
(2)我們在分析解決某些數學問題時,經常要比較兩個數或代數式的大小,而解決問
題的策略一般要進行一定的轉化,其中“作差法”就是常用的方法之一,所謂“作差
法”:就是通過作差、變形,并利用差的符號來確定它們的大小,即要比較代數式M、
N的大小,只要作出它們的差![]() ,若
,若![]() ,則
,則![]() ;若
;若![]() ,則
,則
![]() ;若
;若![]() ,則
,則![]() .
.
請你用“作差法”解決以下問題:用如圖①所示的四塊長方形板材鋪成如圖③的大正方形或如圖④的大長方形,中間分別空出一個小正方形和小長方形(圖中陰影部分);
① 請用含![]() 、
、![]() 的代數式分別表示圖③和圖④中陰影部分的面積;
的代數式分別表示圖③和圖④中陰影部分的面積;
② 試比較圖③和圖④中陰影部分的面積哪個大?大多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點![]() 的坐標
的坐標![]() ,點
,點![]() 的坐標
的坐標![]() ,點
,點![]() 的坐標
的坐標![]() ,點
,點![]() 的坐標
的坐標![]() ,如圖①,另有一點
,如圖①,另有一點![]() 從點
從點![]() 出發,沿著
出發,沿著![]() 運動,到點
運動,到點![]() 停止.
停止.
(![]() )當
)當![]() 在
在![]() 上時,
上時, ![]() __________.
__________.
(![]() )點
)點![]() 在運動過程中,直接寫出可以和
在運動過程中,直接寫出可以和![]() 形成等腰三角形的點的坐標.
形成等腰三角形的點的坐標.
(![]() )將圖①中的長方形在坐標平面內繞原點按逆時針方向旋轉
)將圖①中的長方形在坐標平面內繞原點按逆時針方向旋轉![]() ,如圖②,求出此時點
,如圖②,求出此時點![]() 、
、![]() 、
、![]() 的坐標?
的坐標?


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com