
【題目】如圖,在直角坐標系中,點A在x軸上,且A(4,0),點B在y軸上,且B(0,4).
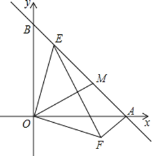
(1)求線段AB的長;
(2)若點E在線段AB上,OE⊥OF,且OE=OF,求AE+AF的值;
(3)在(2)的條件下,過O作OM⊥EF,交AB于M,試確定線段BE、EM、AM之間的數量關系?并證明你的結論.
【答案】(1)AB=4![]() ;
;
(2)AE+AF=4![]() ;
;
(3)結論:FM2=AM2+AF2,理由見解析.
【解析】
(1)根據AB=![]() 即可解決;
即可解決;
(2)先證明△BOE≌△AOF得AF=BE,所以AE+AF=AE+BE=AB即可解決;
(3)結論:FM2=AM2+AF2.只要證明ME=MF,AF=BE,在RT△AMF中利用勾股定理即可證明.
(1)在Rt△ABO中,∵AO=OB=4,
∴AB=![]() =
=![]() =4
=4![]() ;
;
(2)∵∠BOA=∠EOF=90°,
∴∠BOE=∠AOF,
在△BOE和△AOF中,
 ,
,
∴△BOE≌△AOF,
∴AF=BE,
∴AE+AF=AE+EB=AB=4![]() ;
;
(3)結論:FM2=AM2+AF2,理由如下:
連接FM,
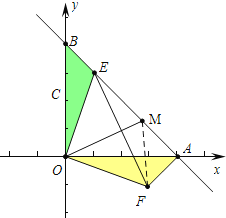
∵OE=OF,OM⊥EF,
∴OM垂直平分分EF,
∴ME=MF,
∵OA=OB,∠AOB=90°,
∴∠OBA=∠OAB=45°,
由(1)可知△BOE≌△AOF,
∴BE=AF,∠OBE=∠OAF=45°,
∴∠MAF=∠OAF+∠OAB=90°,
∴FM2=AM2+AF2,
∴EM2=BE2+AM2.


科目:初中數學 來源: 題型:
【題目】為落實視力保護工作,某校組織七年級學生開展了視力保健活動.活動前隨機測查了30名學生的視力,活動后再次測查這部分學生的視力.兩次相關數據記錄如下:
活動前被測查學生視力數據:
4.0,4.1,4.1,4.2,4.2,4.3,4.3,4.4,4.4,4.4,4.5,4.5,4.6,4.6,4.6
4.7,4.7,4.7,4.7,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,5.0,5.0,5.1
活動后被測查學生視力數據:
4.0,4.2,4.3,4.4,4.4,4.5,4.5,4.6,4.6,4.6,4.7,4.7,4.7,4.7,4.8
4.8,4.8,4.8,4.8,4.8,4.8,4.9,4.9,4.9,4.9,4.9,5.0,5.0,5.1,5.1
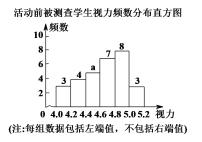

根據以上信息回答下列問題:
(1)填空:a= ,b= ,活動前被測查學生視力樣本數據的中位數是 ,活動后被測查學生視力樣本數據的眾數是 ;
(2)若視力在4.8及以上為達標,估計七年級600名學生活動后視力達標的人數有多少?
(3)分析活動前后相關數據,從一個方面評價學校開展視力保健活動的效果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個相似三角形的面積比為![]() ,周長和是
,周長和是![]() ,則這兩個三角形的周長分別是( )
,則這兩個三角形的周長分別是( )
A. 8cm和12cm B. 7cm和13cm C. 9cm和11cm D. 6cm和14cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠要把一批產品從![]() 地運往
地運往![]() 地,若通過鐵路運輸,則每千米需交運費20元,還要交裝卸費400元及手續費200元,若通過公路運輸,則每千米需要交運費30元,還需交手續費100元(由于本廠職工裝卸,不需交裝卸費).設
地,若通過鐵路運輸,則每千米需交運費20元,還要交裝卸費400元及手續費200元,若通過公路運輸,則每千米需要交運費30元,還需交手續費100元(由于本廠職工裝卸,不需交裝卸費).設![]() 地到
地到![]() 地的路程為
地的路程為![]() ,通過鐵路運輸和通過公路運輸需交總運費
,通過鐵路運輸和通過公路運輸需交總運費![]() 元和
元和![]() 元.
元.
(1)求![]() 和
和![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)若![]() 地到
地到![]() 地的路程為
地的路程為![]() ,哪種運輸可以節省總運費?
,哪種運輸可以節省總運費?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC與BD交于點O.過點C作BD的平行線,過點D作AC的平行線,兩直線相交于點E.
(1)求證:四邊形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面積是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市2017年國內生產總值(GDP)比2016年增長了12%,由于受到國際金融危機的影響,預計2018比2017年增長7%,若這兩年GDP年平均增長率為![]() %,則
%,則![]() %滿足的關系是( )
%滿足的關系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 個世界讀書日,為迎接第
個世界讀書日,為迎接第![]() 個世界讀書日的到來,某校舉辦讀書分享大賽活動:大賽以“推薦分享”為主題,參賽者選擇一本自己最喜歡的書,然后給該書寫一段推薦語、一篇讀書心得、舉辦一場讀書講座.大賽組委會對參賽者提交的推薦語、讀書心得、舉辦的讀書講座進行打分(各項成績均按百分制),綜合成績排名第一的選手將獲得大賽一等獎.現有甲、乙兩位同學的各項成績如下表所示;
個世界讀書日的到來,某校舉辦讀書分享大賽活動:大賽以“推薦分享”為主題,參賽者選擇一本自己最喜歡的書,然后給該書寫一段推薦語、一篇讀書心得、舉辦一場讀書講座.大賽組委會對參賽者提交的推薦語、讀書心得、舉辦的讀書講座進行打分(各項成績均按百分制),綜合成績排名第一的選手將獲得大賽一等獎.現有甲、乙兩位同學的各項成績如下表所示;
參賽者 | 推薦語 | 讀書心得 | 讀書講座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若將三項成績的平均分作為參賽選手的綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
(2)若“推薦語”“讀書心得”“讀書講座”的成績按![]() 確定綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
確定綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司招聘一名員工,現有甲、乙兩人競聘,公司聘請了3位專家和4位群眾代表組成評審組,評審組對兩人竟聘演講進行現場打分,記分采用100分制,其得分如下表:
評委(序號) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙兩位競聘者得分的中位數分別是多少
(2)計算甲、乙兩位應聘者平均得分,從平均得分看應該錄用誰(結果保留一位小數)
(3)現知道1、2、3號評委為專家評委,4、5、6、7號評委為群眾評委,如果對專家評委組與群眾評委組的平均分數分別賦子適當的權,那么對專家評委組賦的權至少為多少時,甲的平均得分比乙的平均得分多0.5分及以上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC內部,且AD=CD,∠ADC=90°,連接BD,若△BCD的面積為10,則AD的長為_____.
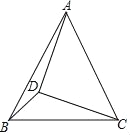
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com